Category Archive: Java
Выгрузка простых чисел
Простые числа длины 1
Простые числа длины 2
Простые числа длины 3
Простые числа длины 4
Простые числа длины 5
Простые числа длины 6
Простые числа длины 7 (первые 10 тысяч чисел)
Простые числа длины 8 (первые 10 тысяч чисел)
Простые числа длины 9 (первые 10 тысяч чисел)
Генерация Java-классов Web-сервиса по WSDL
Допустим, у вас есть WSDL и вы хотите написать либо сам веб-сервис, либо клиента для сервиса. Для этого по WSDL нужно сгенерировать Java-классы с помощью утилиты wsimport, входящую в состав JDK.
Стоит отметить, что сгенерированный код может использовать и на сервере, и на клиенте.
Создайте новую папку и положите в нее вашу WSDL и всё, что к ней относится (это может быть другие WSDL или XSD). Увидеть все, что импортирует ваша основная WSDL можно в теге import. Например:
В данном примере следует заменить интернет адрес XSD на локальный:
Разумеется, файл example.xsd должен лежать c WSDL в одной директории.
Теперь напишем скрипт для генерирования классов. Рассмотрим сперва Windows-версию скрипта, а потом Linux-версию.
Скрипт для Windows
Создайте файл w-gen.bat в любом текстовом редакторе и скопируйте в него следующий код:
cls
set GEN_DIR=kz
rmdir %GEN_DIR% /s/q
"%JAVA_HOME%/bin/wsimport" -keep -Xnocompile -p kz.kesh.blog.v1 myBlog.wsdl
pause
cls - очистка консоли
GEN_DIR - директория пакета верхнего уровня
rmdir - полное удаление директории
wsimport - утилита для генерации Java-классов из WSDL
keep - сохраняет сгенерированные файлы
Xnocompile - не компилирует сгенерированные Java-файлы
kz.kesh.blog.v1 - имя пакета, в котором будет сгенерированые классы
myBlog.wsdl - наша WSDL
pause - пауза, чтобы консольное окно сразу не закрылось
Данный скрипт генерирует *.java файлы, но вы можете немного переработать скрипт и генерировать скопилированные файлы *.class. Так же вы можете доработать упаковку файлов и WSDL в jar. Например:
"%JAVA_HOME%/bin/jar" cf keskBlog.jar kz
jar - стандартная утилита из JDK для создания jar-файлов
cf - создает новый архив с указанным именем
keskBlog.jar - имя вашего jar-файла
kz - директория, которая упаковывается в jar, она соответствует названию верхнего пакета
Скрипт для Linux
Создайте файл w-gen.sh:
#!/bin/bash
GEN_DIR="kz"
rm -r $GEN_DIR
wsimport -keep -Xnocompile -p kz.kesh.blog.v1 myBlog.wsdl
Не забудьте дать скрипту права на выполенение:
chmod +x w-gen.sh
#!/bin/bash - обязательная строчка для bash-скриптов
GEN_DIR - директория пакета верхнего уровня
rm - рекурсивное удаление директории
wsimport - утилита для генерации Java-классов из WSDL
keep - сохраняет сгенерированные файлы
Xnocompile - не компилирует сгенерированные Java-файлы
kz.kesh.blog.v1 - имя пакета, в котором будет сгенерированы классы
myBlog.wsdl - наша WSDL
Вложенный тернарный поиск с золотым сечением
Определение тернарного поиска можно найти в Википедии. Также описание алгоритма можно найти здесь.
Реализация у тернарного поиска несложная, давайте убедимся в этом на примере следующей задачи:
Хотя данную задачу можно решать другими способами, но для учебных целей решим ее тернарным поиском.
Для начала нужно убедиться, что эту задачу вообще можно решить тернарным поиском. Убедимся в унимодальности нашей функции, т.е. на заданном интервале у функции должен быть один экстремум (максимальное или минимальное значение функции на заданном интервале).
Мы будем перебирать углы от 0° до 90°, т.е. наш интервал поиска от 0 до 90. При возрастании угла, начиная от 0°, площадь треугольника строго возрастает, затем при приближении к углу 90° площадь треугольнига строго уменьшается, т.е. у нас есть максимальное значение функции на данном интервале, а значит выполняется унимодальность функции, и мы можем применить тернарный поиск.
Как работает тернарный поиск.
Сначала интервал разбивается на три части, отсюда и название "тернарный" (Ternary переводится как тройной или троичный). На следующем шаге отсеивается участок, в котором точно нет решения, затем снова отрезок разбивается на три части, и это повторяется до тех пор, пока не будет достугнута необходимая точность результата.
Классический способ разбиения - это разбиение на три равные части части:
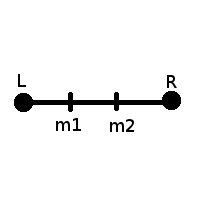 Фрагмент кода, обеспечивающий равенство отрезков Lm1 = m1m2 = m2R:
Фрагмент кода, обеспечивающий равенство отрезков Lm1 = m1m2 = m2R:
 2) Если f(m1) > f(m2), аналогично имеется только два случая, когда максимальное значение лежит в центральной или левой части, а значит правую часть можно отбросить.
2) Если f(m1) > f(m2), аналогично имеется только два случая, когда максимальное значение лежит в центральной или левой части, а значит правую часть можно отбросить.
 3) Если f(m1) = f(m2), то возможен только один вариант, при котором максимальное значение находится в центральной части, а значит левую и правую части можно отбросить.
3) Если f(m1) = f(m2), то возможен только один вариант, при котором максимальное значение находится в центральной части, а значит левую и правую части можно отбросить.
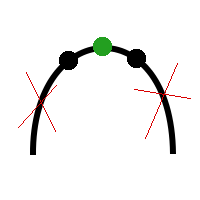 Последний вариант, когда f(m1) = f(m2), в целях облегчения алгоритма можно заменить либо на этот случай f(m1) < f(m2), либо на этот f(m1) > f(m2). В скорости из-за этого, конечно же, мы чуть-чуть проиграем, но выиграем в скорости реализации алгоритма и компактности кода.
После каждого шага алгоритма от исходной области поиска остается 2/3, т.е. не самая большая скорость сходимости. Можно повысить скорость сходимости, если выбирать точки m1 и m2 ближе друг другу, правда при этом теряется точность. Повышение скорости сходимости может потребоваться в случае, когда вычисление функции f(x) занимает много времени и нужно минимизировать кол-во вызовов этой функции.
Очень хорошо при выборе точек m1 и m2 воспользоваться пропорциями золотого сечения. Если тернарный поиск использует пропорции золотого сечения, то это один в один Метод золотого сечения.
Последний вариант, когда f(m1) = f(m2), в целях облегчения алгоритма можно заменить либо на этот случай f(m1) < f(m2), либо на этот f(m1) > f(m2). В скорости из-за этого, конечно же, мы чуть-чуть проиграем, но выиграем в скорости реализации алгоритма и компактности кода.
После каждого шага алгоритма от исходной области поиска остается 2/3, т.е. не самая большая скорость сходимости. Можно повысить скорость сходимости, если выбирать точки m1 и m2 ближе друг другу, правда при этом теряется точность. Повышение скорости сходимости может потребоваться в случае, когда вычисление функции f(x) занимает много времени и нужно минимизировать кол-во вызовов этой функции.
Очень хорошо при выборе точек m1 и m2 воспользоваться пропорциями золотого сечения. Если тернарный поиск использует пропорции золотого сечения, то это один в один Метод золотого сечения.
Золотое сечение - это такое разбиение целого на две части, при котором отношение большего к меньшему равно отношению целого к большему
Это отношение постоянно и равно примерно 1,618, обозначается как φ и называется золотым числом: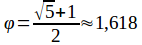 Для вычисления точек m1 и m2, разбивающих область поиска золотым сечением, воспользуемся следующими формулами:
Для вычисления точек m1 и m2, разбивающих область поиска золотым сечением, воспользуемся следующими формулами:
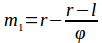
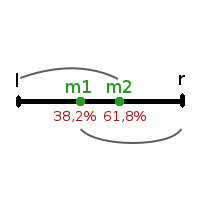
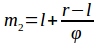 В процентном соотношении длины отрезков lm1 и lm2 приблизительно равны 38,2% и 61,8% от длины отрезка lr.
Благодаря свойствам золотого сечения точка m1 делит отрезок lm2 в пропорциях золотого сечения, а точка m2 делит отрезок m1r также в пропорциях золотого сечения.
В процентном соотношении длины отрезков lm1 и lm2 приблизительно равны 38,2% и 61,8% от длины отрезка lr.
Благодаря свойствам золотого сечения точка m1 делит отрезок lm2 в пропорциях золотого сечения, а точка m2 делит отрезок m1r также в пропорциях золотого сечения.
 И так мы видим, что сходимость золотого сечения будет 0,618, что лучше сходимости в случае разбиения области поиска на равные части, где сходимость у нас была 2/3 (0,66).
А теперь вернемся к решению задачи... Исходный код решения задачи на Java:
И так мы видим, что сходимость золотого сечения будет 0,618, что лучше сходимости в случае разбиения области поиска на равные части, где сходимость у нас была 2/3 (0,66).
А теперь вернемся к решению задачи... Исходный код решения задачи на Java:
 Сперва мы находим углы α1 и α2, которые разбивают область поиска на три равные части (в данной задачи можно не использовать золотое сечение). Далее для угла α1 с помощью вложенного тернарного поиска ищем угол β1, при котором площадь фигуры максимальна, аналогично, для угла α2 находим подходящий угол β2.
Сперва мы находим углы α1 и α2, которые разбивают область поиска на три равные части (в данной задачи можно не использовать золотое сечение). Далее для угла α1 с помощью вложенного тернарного поиска ищем угол β1, при котором площадь фигуры максимальна, аналогично, для угла α2 находим подходящий угол β2.
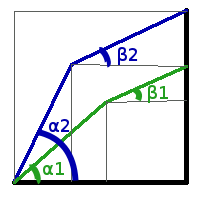 Найдя пары углов α1 и β1; α2 и β2, вычисляем площадь S1 и S2 соответственно. Можно использовать следующую формулу вычисления площади, где a и b - длины палок:
Найдя пары углов α1 и β1; α2 и β2, вычисляем площадь S1 и S2 соответственно. Можно использовать следующую формулу вычисления площади, где a и b - длины палок:
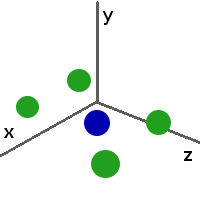 По условию задачи нам нужно вычислить координаты x,y,z строительства новой спасательной станции, причем расстояние от станции до самой дальней планеты должно быть минимально.
Сперва пробуем подобрать координату x тернарным поиском, но координаты y и z - неизвестны, поэтому зафиксировав некоторые точки x, полученные золотым сечением, мы запускаем вложенные тернарный поиск с фиксированной координатой x для поиска координаты y. Далее внутри поиска y запускаем вложенный тернарный поиск координаты z. Когда мы имеем все три зафиксированные координаты мы можем посчитать расстояния до всех планет и из них определить максимальное расстояние, это расстояние и будет значением функции f(x,y,z).
Т.к. в условии сказано, что количество планет может быть 100, то вычисление функции f(x,y,z) очень затратно по времени. Чтобы программа уложилась во временные рамки, нужно при тернарном поиске разбивать область поиска золотым сечением, а не на равные части. Тем самым у нас повыситься сходимость, т.е. вызовов функции f(x,y,z) станет меньше. Но при золотом сечении теряется точность, поэтому мы увеличим точность с 10-6 до 10-7.
Реализация на Java:
По условию задачи нам нужно вычислить координаты x,y,z строительства новой спасательной станции, причем расстояние от станции до самой дальней планеты должно быть минимально.
Сперва пробуем подобрать координату x тернарным поиском, но координаты y и z - неизвестны, поэтому зафиксировав некоторые точки x, полученные золотым сечением, мы запускаем вложенные тернарный поиск с фиксированной координатой x для поиска координаты y. Далее внутри поиска y запускаем вложенный тернарный поиск координаты z. Когда мы имеем все три зафиксированные координаты мы можем посчитать расстояния до всех планет и из них определить максимальное расстояние, это расстояние и будет значением функции f(x,y,z).
Т.к. в условии сказано, что количество планет может быть 100, то вычисление функции f(x,y,z) очень затратно по времени. Чтобы программа уложилась во временные рамки, нужно при тернарном поиске разбивать область поиска золотым сечением, а не на равные части. Тем самым у нас повыситься сходимость, т.е. вызовов функции f(x,y,z) станет меньше. Но при золотом сечении теряется точность, поэтому мы увеличим точность с 10-6 до 10-7.
Реализация на Java:
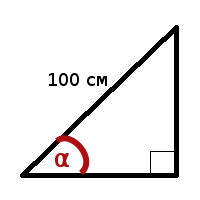
| Имеется прямоугольный треугольник, у которого гипотенуза равна 100 сантиметрам. Нужно вычислить при каком угле α площадь треугольника будет максимальна. |
 Фрагмент кода, обеспечивающий равенство отрезков Lm1 = m1m2 = m2R:
Фрагмент кода, обеспечивающий равенство отрезков Lm1 = m1m2 = m2R:
double m1 = l + (r - l) / 3;
double m2 = r - (r - l) / 3;
При сравнении значений функций в точках m1 и m2 у нас возможно три варианта:
1) Мы сдвигаем область поиска вправо, т.е. l становится равным m1 (l = m1);
2) Мы сдвигаем область поиска влево, т.е. r становится равным m2 (r = m2);
3) При равенстве значений функции в обеих точках, мы сдвигаем область поиска с обеих сторон, т.е. l становиться равным m1 (l = m1), а r становиться равным m2 (r = m2)
Рассмотрим данные случаи на примере поиска максимального значения.
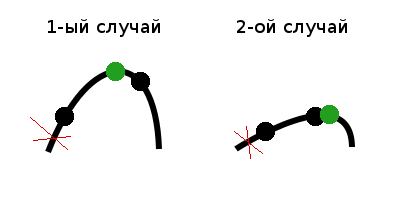
1) Если f(m1) < f(m2), возможно два случая: когда максимальное значение лежит в центральной части или в правой части, а значит левую часть можно отбросить. Максимальное значение обозначено зеленой точкой.
 2) Если f(m1) > f(m2), аналогично имеется только два случая, когда максимальное значение лежит в центральной или левой части, а значит правую часть можно отбросить.
2) Если f(m1) > f(m2), аналогично имеется только два случая, когда максимальное значение лежит в центральной или левой части, а значит правую часть можно отбросить.
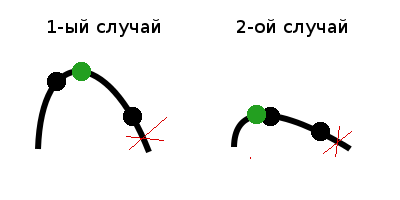
 3) Если f(m1) = f(m2), то возможен только один вариант, при котором максимальное значение находится в центральной части, а значит левую и правую части можно отбросить.
3) Если f(m1) = f(m2), то возможен только один вариант, при котором максимальное значение находится в центральной части, а значит левую и правую части можно отбросить.
 Последний вариант, когда f(m1) = f(m2), в целях облегчения алгоритма можно заменить либо на этот случай f(m1) < f(m2), либо на этот f(m1) > f(m2). В скорости из-за этого, конечно же, мы чуть-чуть проиграем, но выиграем в скорости реализации алгоритма и компактности кода.
После каждого шага алгоритма от исходной области поиска остается 2/3, т.е. не самая большая скорость сходимости. Можно повысить скорость сходимости, если выбирать точки m1 и m2 ближе друг другу, правда при этом теряется точность. Повышение скорости сходимости может потребоваться в случае, когда вычисление функции f(x) занимает много времени и нужно минимизировать кол-во вызовов этой функции.
Очень хорошо при выборе точек m1 и m2 воспользоваться пропорциями золотого сечения. Если тернарный поиск использует пропорции золотого сечения, то это один в один Метод золотого сечения.
Последний вариант, когда f(m1) = f(m2), в целях облегчения алгоритма можно заменить либо на этот случай f(m1) < f(m2), либо на этот f(m1) > f(m2). В скорости из-за этого, конечно же, мы чуть-чуть проиграем, но выиграем в скорости реализации алгоритма и компактности кода.
После каждого шага алгоритма от исходной области поиска остается 2/3, т.е. не самая большая скорость сходимости. Можно повысить скорость сходимости, если выбирать точки m1 и m2 ближе друг другу, правда при этом теряется точность. Повышение скорости сходимости может потребоваться в случае, когда вычисление функции f(x) занимает много времени и нужно минимизировать кол-во вызовов этой функции.
Очень хорошо при выборе точек m1 и m2 воспользоваться пропорциями золотого сечения. Если тернарный поиск использует пропорции золотого сечения, то это один в один Метод золотого сечения.
Золотое сечение - это такое разбиение целого на две части, при котором отношение большего к меньшему равно отношению целого к большему
Это отношение постоянно и равно примерно 1,618, обозначается как φ и называется золотым числом:
 И так мы видим, что сходимость золотого сечения будет 0,618, что лучше сходимости в случае разбиения области поиска на равные части, где сходимость у нас была 2/3 (0,66).
А теперь вернемся к решению задачи... Исходный код решения задачи на Java:
И так мы видим, что сходимость золотого сечения будет 0,618, что лучше сходимости в случае разбиения области поиска на равные части, где сходимость у нас была 2/3 (0,66).
А теперь вернемся к решению задачи... Исходный код решения задачи на Java:
import static java.lang.Math.*;
public class angle {
public static void main(String[] args) {
double l = 0;
double r = 90;
double EPS = 1e-6;//точность 0.000001
double hypo = 100;//гипотенуза
while(r - l >= EPS){//повторяем цикл пока не достигнем требуемой точности
double m1 = l + (r - l) / 3;
double m2 = r - (r - l) / 3;
if(f(hypo,m1) < f(hypo,m2)){
l = m1;
}else{
r = m2;
}
}
System.out.println((l + r) / 2);//результат 44.99999993498489
}
//функция расчета площади треугольника по гипотенузе и углу
static double f(double hypo,double alpha){
alpha = toRadians(alpha);
return 0.5 * hypo * hypo * cos(alpha) * sin(alpha);
}
}
Т.е. при угле в 44.999999° (45°) достигается максимальная площадь треугольника. В качестве ответа можно было взять значение из переменной l или r, это возможно благодаря достижению заданной точности результата, также можно взять их середину (l + r) / 2, как в рассмотренном выше коде.
Задача на вложенный тернарный поиск
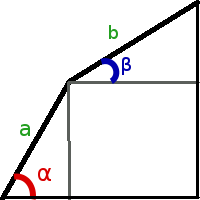
В качестве примера применения вложенного тернарного поиска возьмем задачу "Футбольные ворота". С условием задачи можно ознакомиться здесь или здесь.
Найти максимальную площадь ворот можно, подобрав углы для палок α и β:
 Сперва мы находим углы α1 и α2, которые разбивают область поиска на три равные части (в данной задачи можно не использовать золотое сечение). Далее для угла α1 с помощью вложенного тернарного поиска ищем угол β1, при котором площадь фигуры максимальна, аналогично, для угла α2 находим подходящий угол β2.
Сперва мы находим углы α1 и α2, которые разбивают область поиска на три равные части (в данной задачи можно не использовать золотое сечение). Далее для угла α1 с помощью вложенного тернарного поиска ищем угол β1, при котором площадь фигуры максимальна, аналогично, для угла α2 находим подходящий угол β2.
 Найдя пары углов α1 и β1; α2 и β2, вычисляем площадь S1 и S2 соответственно. Можно использовать следующую формулу вычисления площади, где a и b - длины палок:
Найдя пары углов α1 и β1; α2 и β2, вычисляем площадь S1 и S2 соответственно. Можно использовать следующую формулу вычисления площади, где a и b - длины палок:
S = 0.5 * a * a * cos(alpha) * sin(alpha) + 0.5 * b * b * cos(beta) * sin(beta) + a * b * sin(alpha) * cos(beta)Сравнив полученные площади, мы можем отсеять треть диапазона углов, которые дают маленькую площадь. И повторяем эти шаги до тех пор, пока не достигнем требуемой точности. Код решения задачи на Java:
import java.io.*;
import static java.lang.Math.*;
import java.text.DecimalFormat;
import java.text.DecimalFormatSymbols;
import java.util.*;
public class FooballGate {
static int a;//длина 1-ой палки
static int b;//длина 2-ой палки
static double EPS = 1e-6;//точность результата
public static void main(String[] args) throws IOException {
Scanner s = new Scanner(new File("input.txt"));
s.useLocale(Locale.US);
a = s.nextInt();
b = s.nextInt();
s.close();
double l = 0;
double r = 90;
while(r - l >= EPS){
double m1 = l + (r - l) / 3;
double m2 = r - (r - l) / 3;
if(f(m1) < f(m2)){
l = m1;
}else{
r = m2;
}
}
double ans = f((l + r) / 2);//результат
DecimalFormat df = new DecimalFormat("0.00000000",
DecimalFormatSymbols.getInstance(Locale.US));
System.out.println(df.format(ans));//вывод с восемью знаками после запятой
}
//функция расчета площади с фиксированным углом alpha,
//в которой тернарным поиском идет поиск угла beta,
//при котором площадь максимальна
static double f(double alpha){
double l = 0;
double r = 90;
while(r - l >= EPS){
double m1 = l + (r - l) / 3;
double m2 = r - (r - l) / 3;
if(f(alpha,l) < f(alpha,r)){
l = m1;
}else{
r = m2;
}
}
return f(alpha,(l + r) / 2);
}
//функция расчета площади в зависимости от углов: alpha и beta
static double f(double alpha, double beta){
alpha = toRadians(alpha);
beta = toRadians(beta);
return 0.5 * a * a * cos(alpha) * sin(alpha) +
0.5 * b * b * cos(beta) * sin(beta) +
a * b * sin(alpha) * cos(beta);
}
}
Задача на тройную вложенность тернарного поиска с необходимостью применения золотого сечения
Задача называется "Космические спасатели". Ознакомиться с условием задачи можно здесь или здесь.
 По условию задачи нам нужно вычислить координаты x,y,z строительства новой спасательной станции, причем расстояние от станции до самой дальней планеты должно быть минимально.
Сперва пробуем подобрать координату x тернарным поиском, но координаты y и z - неизвестны, поэтому зафиксировав некоторые точки x, полученные золотым сечением, мы запускаем вложенные тернарный поиск с фиксированной координатой x для поиска координаты y. Далее внутри поиска y запускаем вложенный тернарный поиск координаты z. Когда мы имеем все три зафиксированные координаты мы можем посчитать расстояния до всех планет и из них определить максимальное расстояние, это расстояние и будет значением функции f(x,y,z).
Т.к. в условии сказано, что количество планет может быть 100, то вычисление функции f(x,y,z) очень затратно по времени. Чтобы программа уложилась во временные рамки, нужно при тернарном поиске разбивать область поиска золотым сечением, а не на равные части. Тем самым у нас повыситься сходимость, т.е. вызовов функции f(x,y,z) станет меньше. Но при золотом сечении теряется точность, поэтому мы увеличим точность с 10-6 до 10-7.
Реализация на Java:
По условию задачи нам нужно вычислить координаты x,y,z строительства новой спасательной станции, причем расстояние от станции до самой дальней планеты должно быть минимально.
Сперва пробуем подобрать координату x тернарным поиском, но координаты y и z - неизвестны, поэтому зафиксировав некоторые точки x, полученные золотым сечением, мы запускаем вложенные тернарный поиск с фиксированной координатой x для поиска координаты y. Далее внутри поиска y запускаем вложенный тернарный поиск координаты z. Когда мы имеем все три зафиксированные координаты мы можем посчитать расстояния до всех планет и из них определить максимальное расстояние, это расстояние и будет значением функции f(x,y,z).
Т.к. в условии сказано, что количество планет может быть 100, то вычисление функции f(x,y,z) очень затратно по времени. Чтобы программа уложилась во временные рамки, нужно при тернарном поиске разбивать область поиска золотым сечением, а не на равные части. Тем самым у нас повыситься сходимость, т.е. вызовов функции f(x,y,z) станет меньше. Но при золотом сечении теряется точность, поэтому мы увеличим точность с 10-6 до 10-7.
Реализация на Java:
import java.io.*;
import java.text.DecimalFormat;
import java.text.DecimalFormatSymbols;
import java.util.*;
public class SpaceRescuers {
static int MAX = (int) 1e4;//максимальная граница поиска
static int MIN = -MAX;//минимальная граница поиска
static class Point{
int x;
int y;
int z;
public Point(int x, int y, int z) {
super();
this.x = x;
this.y = y;
this.z = z;
}
}
static class PointD{
double x;
double y;
double z;
public PointD(double x, double y, double z) {
super();
this.x = x;
this.y = y;
this.z = z;
}
}
static Point[] points;
static double EPS = 1e-7;
static PointD bestPoint;//лучшая точка
static double best = Double.MAX_VALUE;//лучшее расстояние (минимальное)
static double fi = 1 / ((Math.sqrt(5) + 1) / 2);
public static void main(String[] args) throws IOException {
Scanner s = new Scanner(new File("input.txt"));
s.useLocale(Locale.US);
int N = s.nextInt();
points = new Point[N];
for(int i = 0; i < N; i++){
points[i] = new Point(s.nextInt(),s.nextInt(),s.nextInt());
}
s.close();
double l = MIN;
double r = MAX;
while(r - l > EPS){
double delta = (r - l) * fi;
double m1 = r - delta;
double m2 = l + delta;
if(f(m1) > f(m2)){
l = m1;
}else{
r = m2;
}
}
double x = bestPoint.x;
double y = bestPoint.y;
double z = bestPoint.z;
DecimalFormat df = new DecimalFormat("0.000000",
DecimalFormatSymbols.getInstance(Locale.US));
System.out.println(df.format(x) + " " + df.format(y) + " " +
df.format(z));
}
//опредение минимального расстояния при фиксированной координате x
static double f(double x){
double l = MIN;
double r = MAX;
while(r - l > EPS){
double delta = (r - l) * fi;
double m1 = r - delta;
double m2 = l + delta;
if(f(x,m1) > f(x,m2)){
l = m1;
}else{
r = m2;
}
}
return f(x,(l + r) / 2);
}
//определение минимального расстояния при фиксированных координатах x и y
static double f(double x,double y){
double l = MIN;
double r = MAX;
while(r - l > EPS){
double delta = (r - l) * fi;
double m1 = r - delta;
double m2 = l + delta;
if(f(x,y,m1) > f(x,y,m2)){
l = m1;
}else{
r = m2;
}
}
return f(x,y,(l + r) / 2);
}
//определение минимального расстояния при фиксированных координатах x,y и z
static double f(double x,double y,double z){
double max = 0;
for(int i = 0; i < points.length; i++){
Point p = points[i];
double s =
(p.x - x) * (p.x - x) +
(p.y - y) * (p.y - y) +
(p.z - z) * (p.z - z);
max = Math.max(max, s);
}
if(max < best){
best = max;
bestPoint = new PointD(x,y,z);
}
return max;
}
}
Обратите внимание на некоторые места в коде:
- Мы рассчитываем не φ, а 1/φ, чтобы дальше в вычислениях использовать умножение, а не деление, т.к. умножение работает быстрее;
static double fi = 1 / ((Math.sqrt(5) + 1) / 2);
double delta = (r - l) * fi; double m1 = r - delta; double m2 = l + delta;
- В первых двух задачах мы рассматривали поиск максимального значения, а данной задаче нас интересует минимально значение, поэтому в условном операторе меняется условие:
if(f(m1) > f(m2)){ l = m1; }else{ r = m2; } - Обратите внимание, что при расчете расстояния извлечение квадратного корня опущено.
double s = (p.x - x) * (p.x - x) + (p.y - y) * (p.y - y) + (p.z - z) * (p.z - z);
Извлечение квадратног корня - очень затратная операция. Сравнивать расстояния можно и без извлечения корня, а если бы потребовалось узнать самое минимальное расстояние, то корень можно было бы извлечь в самом конце.
Перебор всех возможных вариантов
В данной статье будет рассмотрено два алгоритма перебора всех возможных вариантов.
Для начала придумаем задачу, на примере которой будем рассматривать алгоритмы.
Пусть у нас имеется множество S, состоящее из 4-х элементов: * - + /, и наша задача - перебрать все возможные комбинации из 3-х элементов, используя элементы множества S. Причем, выбираемые элементы могут повторяться. Например: "+*+".
Первый алгоритм
Сопоставим каждому элементу число, начиная с 0.
* - 0
- - 1
+ - 2
/ - 3
Можно догадаться, что нужно перебрать элементы от 0 0 0 до 3 3 3:
0 0 0
0 0 1
0 0 2
0 0 3
0 1 0
0 0 1
...
...
3 2 3
3 3 0
3 3 1
3 3 2
3 3 3
Всего получится 64 варианта (4 * 4 * 4 = 64)
Далее нужно провести обратную операцию, сопоставив числу элемент множества S.
Например, набору 2 0 2 соответствует +*+
В алгоритме мы будем имитировать сложение в столбик, каждый раз прибавляя единицу, чтобы получить новый вариант.
Реализация:
char abc[] = new char[]{'*','-','+','/'};//множество допустимых символов
int size = 3;//кол-во элементов
int arr[] = new int[size];//массив для хранения текущего варианта множества
outer: while(true){//вечный цикл
//вывод варианта множества на экран
for(int ndx : arr){
System.out.print(abc[ndx]);
}
System.out.println();
int i = size - 1;//ставим курсов в самую правую ячейку
while(arr[i] == abc.length - 1){//движемся влево, если ячейка переполнена
arr[i] = 0;//записываем в ячейку 0, т.к. идет перенос разряда
i--;//сдвиг влево
//если перенос влево невозможен, значит перебор закончен
if(i < 0)break outer;
}
arr[i]++;//увеличиваем значение ячейки на единицу
}
В результате программа выведет все 64 варианта:
*** **- **+ **/ *-* *-- ... ... /++ /+/ //* //- //+ ///Второй алгоритм Для начала посчитаем сколько всего возможных комбинаций, это число равно n ^ k, где n - это размер алфавита (кол-во допустимых символов), а k - кол-во элементов в комбинации. Для нашего множества S, состоящего из *,-,+ и /, n равно 4. И т.к. нужно перебрать все комбинации из трех элементов, то k равно 3. Получаем: n ^ k = 4 ^ 3 = 64. В итоге мы должны получить 64 комбинации. Вот если бы существовал способ преобразования номера комбинации в элементы комбинации. И такой способ существует: для этого нужно номер комбинации преобразовать в k-значное число в системе счисления по основанию n. Первой комбинации будет соответствовать число 0, а последней 63. Перебирая числа от 0 до 63, нам нужно каждое число преобразовать в число в систему счисления по основанию 4. Для получения разрядов числа нужно целочисленно разделить число на 1, 4, 16 (т.е. n^0, n^1, n^2) и результат взять по модулю n. Пример: для числа 57 при k = 3 и n = 4 (57 / 1) % 4 = 57 % 4 = 1 (-) (57 / 4) % 4 = 14 % 4 = 2 (+) (57 / 16) % 4 = 3 % 4 = 3 (/) Т.е. комбинации под номером 57 соответствует комбинация -+/
char abc[] = new char[]{'*','-','+','/'};//множество допустимых символов (алфавит)
int N = abc.length;//N - размер алфавита
int K = 3;//кол-во элементов в комбинации
int pow[] = new int[K + 1];//массив для степеней числа N: N^0, N^1, .., N^K
pow[0] = 1;
for (int i = 1; i <= K; i++) {//вычисляем степени числа N
pow[i] = pow[i - 1] * N
}
//перебираем все номера комбинаций
for (int i = 0; i < pow[K]; i++) {
char arr[] = new char[K];
//вычисляем элементы комбинации
for (int j = 0; j < K; j++) {
//каждый элемент получаем из массива abc по индексу,
//индекс - это число в системе счисления по основанию N (0..N-1)
//в соответствующем разряде j (от 0 до K-1 включительно)
arr[j] = abc[(i / pow[j]) % N];
}
//вывод в консоль
for(char ch : arr){
System.out.print(ch);
}
System.out.println();
}
Вывод программы:
0 *** 1 -** 2 +** 3 /** 4 *-* ..... 57 -+/ 58 ++/ 59 /+/ 60 *// 61 -// 62 +// 63 ///В данном алгоритме перебор идет как бы слева направо, но это не важно, т.к. мы перебираем все комбинации.
Перебор всех подмножеств заданного множества (Java)
Пусть дано множество, состоящее из четырех элементов: {a,b,c,d}.
Необходимо перебрать все возможные подмножества данного множества:
1) {} - пустое множество
2) {a}
3) {b}
4) {a,b}
5) {c}
6) {a,c}
7) {b,c}
8) {a,b,c}
9) {d}
10) {a,d}
11) {b,d}
12) {a,b,d}
13) {c,d}
14) {a,c,d}
15) {b,c,d}
16) {a,b,c,d}
Причем подмножества {a,b} и {b,a} считаются одним и тем же подмножеством.
Данную задачу будем решать с использованием битовых масок и битовых операций.
Сразу приведу реализацию:
char arr[] = new char[]{'a','b','c','d'};
int N = arr.length;
for (int mask = 0; mask < (1 << N); mask++) {//перебор масок
for (int j = 0; j < N; j++) {//перебор индексов массива
if((mask & (1 << j)) != 0){//поиск индекса в маске
System.out.print(arr[j] + " ");//вывод элемента
}
}
System.out.println();//перевод строки для вывод следующего подмножества
}
А теперь пояснения.
1 << N - побитовый сдвиг единицы на N позиций влево.
В двоичном виде единица выглядит так 00000001. В нашем случае N = 4.
После сдвига на 4 позиции влево появится новое число, двоичный вид которого 00010000. Теперь, если вычесть из этого числа единицу получим: 00001111. Если опустить ведущие нули, то получим 1111. Четыре единицы - это состояние, когда в подмножество попадают все элементы, 0000 - пустое множество, 1010 - подмножество состоит из первого и третьего элемента множества (нумерация с нуля, отсчет ведется справа) и т.д.
Т.е. мы перебираем числа, двоичное представление которых от 0000 до 1111.
После того как мы получили маску (mask), необходимо узнать в каких позициях стоят единицы. Проверять будем следующим образом.
Например, на каком-то шаге цикла программы маска равна 1100, мы перебираем все позиции путем сдвига единицы: 0001, 0010, 0100 и 1000. Для проверки воспользуемся операцией побитового И (если в одинаковых позициях стоят единицы, то результат единица, иначе ноль). В Java обозначается как &
В нашем случае:
1100 & 0001 = 0000
1100 & 0010 = 0000
1100 & 0100 = 0100
1100 & 1000 = 1000
Т.е. если в итоге получилось число отличное от нуля, то включаем элемент в множество.
0100 - включаем в множество элемент с индексом 2
1000 - включаем в множество элемент с индексом 3
Нумерация с нуля и справа.
Результат работы программы (первая строка пустая - это пустое множество):
a b a b c a c b c a b c d a d b d a b d c d a c d b c d a b c dВ данной реализации мы хранили маски в типе int. (1 << 30) равно 1 073 741 824 Безопасное значение N для типа int: 30. Свыше 30 будет переполнение переменных типа int, поэтому нужно использовать long. При N > 30 перебор будет ощутимо все медленнее и медленнее. Если будете делать реализацию с long, то при сдвиге единицы нужно писать так:
1L << j
Т.е. нужно к единице приписать L, и тогда результат операции будет long, в противном случае будет int с переполнением. Замена и удаление повторяющихся символов в строке
В данной статье будет рассмотрена замена и удаление повторяющихся символов в строке с помощью регулярных выражений Java.
Заменять и удалять повторяющиеся символы будет через функции замены класса String.
У класса String есть четыре метода для замены символов. Вот их сигнатуры:
- replace(char oldChar, char newChar):String
- replace(CharSequence target, CharSequence replacement):String
- replaceAll(String regex,String replacement):String
- replaceFirst(String regex,String replacement):String
- Представим себе следующую задачу: требуется удалить из строки все стоящие рядом два одинаковых символа. Например, из строки "keeshh" должна в итоге получиться строка "ks"
String text = "keeshh"; String result = text.replaceAll("([a-z])\\1", ""); System.out.println(result);//"ks"replaceAll - функция для замены всех совпадений [a-z] - выражение говорит о том, что на этом месте должен быть символ в диапазоне от a до z. () - круглые скобки означают группировку, сослаться на которую можно по номеру, причем нумерация начинается с единицы \1 - указывает на то, что в этом месте должен быть такой же текст, как в группировке под номером 1. Обратный слэш "\" необходимо экранировать, поэтому в выражении два слэша "\\" - После удаление двух повторных символов, могут снова образоваться повторные символы.
Например, если в строке "keeshhs" заменить два подряд повторяющихся символа, то получится "kss", но подстроку "ss" также можно удалить. Поместим описанный выше код в цикл, который будет повторяться до тех пор, пока не будут заменены все повторные символы. В данной реализации будем пытаться удалять повторения, пока меняется (укорачивается) длина строки
String text = "keeshhs"; int len; do{ len = text.length();//сохраняем длину строки text = text.replaceAll("([a-z])\\1", ""); }while(len != text.length());//сравниваем новую длину строки с сохраненной длиной System.out.println(text);//"k" - Рассмотрим следующий пример. Нужно удалить все повторяющиеся подряд символы.
Например, для строки "keeeshh" результат должен быть "ks". Реализация:
String text = "keeeeshh"; text = text.replaceAll("([a-z])\\1+", ""); System.out.println(text);//"ks"Как вы, наверное, заметили после единички добавился символ +. Плюс в регулярных означает, что предшествующий плюсу символ или группировка должна встретиться от одного раза и более. Можно также включить этот код в цикл, чтобы снова заменить появившиеся повторения. - Теперь рассмотрим замену. Задача: имеется строка, необходимо из двух подряд идущих одинаковых символов оставить только один.
Пример: из строки "kkeesshh" получится строка "kesh".
Реализация:
String text = "kkeesshh"; text = text.replaceAll("([a-z])\\1", "$1"); System.out.println(text);//"kesh"Для замены мы использовали выражение $1, которое говорит о том, что текст, соответствующий регулярному выражению, необходимо заменить на текст, соответствующий группировке с номером 1. В нашем случае группировка с номером - это текст, соответствующий шаблону [a-z]. Можно переписать код, используя группу с номером 2 для замены:String text = "kkeesshh"; text = text.replaceAll("([a-z])(\\1)", "$2"); System.out.println(text);//"kesh"Вторая группа соответствует шаблону \\1 - И напоследок заменим в строке все подряд повторяющиеся символы одним символом.
Например, строка "keeeeessshh" преобразуется в "kesh".
Реализация:
String text = "keeeeessshh"; text = text.replaceAll("([a-z])\\1+", "$1"); System.out.println(text);//"kesh"
org.apache.http.NoHttpResponseException: The target server failed to respond
Случилось так, что в двух моих Android-приложениях перестала работать статистика. Хотя приложения уже работали более года без обновлений, да и сервис статистики я не трогал.
Запустив одно из приложений под отладкой, обнаружил ошибку:
org.apache.http.NoHttpResponseException: The target server failed to respondПотом локализовал ошибку. Вот фрагмент проблемного кода:
HttpParams httpParams = new BasicHttpParams();
HttpConnectionParams.setConnectionTimeout(httpParams, 5000);//тайм-аут подключения
HttpConnectionParams.setSoTimeout(httpParams, 10000);//тайм-аут сокета
HttpClient httpClient = new DefaultHttpClient(httpParams);
HttpGet httpGet = new HttpGet(url);
HttpResponse httpResponse = httpClient.execute(httpGet);//тут выбрасывается Exception
Попробовал переписать код так (без HTTP-параметров).:
HttpClient httpClient = new DefaultHttpClient();
HttpGet httpGet = new HttpGet(url);
HttpResponse httpResponse = httpClient.execute(httpGet);
Статистика в приложении начала работать. Т.е. дело оказалось в передаваемых параметрах. Мне кажется, провайдер хостинга что-то обновил, и теперь сервер перестал понимать передаваемые запросы.
Погуглив, нашел другой способ передачи параметров, способ - работает!
HttpClient httpClient = new DefaultHttpClient();
httpClient.getParams().setParameter(HttpConnectionParams.CONNECTION_TIMEOUT, 5000);
httpClient.getParams().setParameter(HttpConnectionParams.SO_TIMEOUT, 10000);
HttpGet httpGet = new HttpGet(url);
HttpResponse httpResponse = httpClient.execute(httpGet);
Как видно из приведенного выше кода:
- Нужно создать объект HttpClient, используя конструктор без параметров DefaultHttpClient()
- С помощью httpClient.getParams().setParameter(String name,Object value) установить необходимые параметры
Сделать в слове первую букву заглавной (Java)
Для того чтобы сделать первую букву в слове заглавной, напишем собственную функцию firstUpperCase. Функция firstUpperCase будет принимать слово, а возвращать тоже слово, но с первой заглавной буквой.
public String firstUpperCase(String word){
if(word == null || word.isEmpty()) return "";//или return word;
return word.substring(0, 1).toUpperCase() + word.substring(1);
}
word.substring(0, 1) - возвращает первую букву в слове
word.substring(0, 1).toUpperCase() - переводит первую букву в верхний регистр
word.substring(1) - добавляет остальные символы без изменения
Пример использования:
String var = "name";
System.out.println("get" + firstUpperCase(var) + "()");//Выведет: "getName()"
FastScanner — ускоряем чтение данных
Стандартный класс Scanner из пакета java.util очень хорош для чтения небольшого кол-ва данных, но если кол-во данных большое и скорость чтения критична, то нужно самостоятельно реализовать более быстрый сканер. Ниже приведен пример такого сканера.
import java.io.*;
import java.util.StringTokenizer;
public class FastScanner {
BufferedReader br;
StringTokenizer st;
public FastScanner(){
init();
}
public FastScanner(String name) {
init(name);
}
public FastScanner(boolean isOnlineJudge){
if(!isOnlineJudge || System.getProperty("ONLINE_JUDGE") != null){
init();
}else{
init("input.txt");
}
}
private void init(){
br = new BufferedReader(new InputStreamReader(System.in));
}
private void init(String name){
try {
br = new BufferedReader(new FileReader(name));
} catch (FileNotFoundException e) {
e.printStackTrace();
}
}
public String nextToken(){
while(st == null || !st.hasMoreElements()){
try {
st = new StringTokenizer(br.readLine());
} catch (IOException e) {
e.printStackTrace();
}
}
return st.nextToken();
}
public int nextInt(){
return Integer.parseInt(nextToken());
}
public long nextLong(){
return Long.parseLong(nextToken());
}
public double nextDouble(){
return Double.parseDouble(nextToken());
}
}
Примеры использования
Объявление FastScanner'а для чтения из консоли:
FastScanner scan = new FastScanner();
Объявление FastScanner'а для чтения из указанного файла:
FastScanner scan = new FastScanner("A.in");
Объявление FastScanner'а для чтения из консоли или из файла input.txt
в зависимости от установленного свойства ONLINE_JUDGE
FastScanner scan = new FastScanner(true);
Чтение данных:
int i = scan.nextInt();
long l = scan.nextLong();
double d = scan.nextDouble();
String token = scan.nextToken();
Быстрый вывод в консоль
Наряду с быстрым чтением входных данных, также важен быстрый вывод данных в консоль. Для ускорения вывода будем не сразу выводить данные в консоль с помощью System.out, а с помощью PrintWriter будем накапливать, и лишь потом сбрасывать данные в консоль командой flush (что эффективнее). Сбрасывать данные лучше порциями среднего размера, чтобы соблюсти баланс между скорость и потребляемой памятью.
PrintWriter out = new PrintWriter(System.out);
out.println(result);
out.flush();
Сравним вывод одинаковых данных через обычный System.out и через PrintWriter.
Код ниже у меня отработал примерно за 2 секунды:
for (int i = 0; i < 1000; i++) {
for (int j = 0; j < 1000; j++) {
System.out.println(i * j);
}
}
А следующий код с буферизацией отработал существенно быстрее, за менее чем 0,7 секунды:
PrintWriter out = new PrintWriter(System.out);
for (int i = 0; i < 1000; i++) {
for (int j = 0; j < 1000; j++) {
out.println(i * j);
}
out.flush();
}
Вывод числа с точностью до заданного количества цифр после запятой
Иногда требуется вывести определенное количество цифр после запятой, даже если цифры - концевые нули.
Данную задачу решает класс DecimalFormat, которому в конструктор класса необходимо передать шаблон числа.
Рассмотрим несколько вариантов использования:
1) Пример округления до трех знаков
DecimalFormat df = new DecimalFormat("0.000");
System.out.println(df.format(13.6784));//результат 13,678
System.out.println(df.format(13.6785));//результат 13,678
System.out.println(df.format(13.67851));//результат 13,679
System.out.println(df.format(13));//результат 13,000
Разделителем между целой и дробной частью в данном случае выступает запятая, но это зависит от текущей локализации.
Если в качестве разделителя требуется точка, то можем это сделать, указав американскую локализацию.
2) Округление до двух знаков и американская локализация
DecimalFormat df = new DecimalFormat("0.00",DecimalFormatSymbols.getInstance(Locale.US));
System.out.println(df.format(13.6749));//результат 13.67
System.out.println(df.format(13.6750));//результат 13.68
System.out.println(df.format(13.6751));//результат 13.68
System.out.println(df.format(13));//результат 13.00
3) Если вы были внимательны, то могли заменить, что округление работает странным образом.
Например,
System.out.println(df.format(13.6785));//результат 13,678
Хотя ожидаемый ответ: 13,679.
Все дело в том, что по умолчанию используется округление HALF_EVEN, где округление идет в сторону ближайшего четного. Это так называемое "Округление банкиров", которое используется главным образом в США. Такой способ округления позволяет снизить накопление ошибок при округлении.
Рассмотрим пример: дробные части .49 и .51 уравновешивают друг друга, одно число округляется в меньшую, а второй в большую строну. Но как быть с дробной частью .50, которая, допустим, всегда увеличивается в большую строну. Для этого придумали следующую систему: смотрим соседнее число, если число нечетно, то округляем в большую сторону; если четное, то округляем в меньшую сторону. Или проще говоря, округляем половину до ближайшего четного числа. Рассмотрим два случая:
1) Число 13.6785 после округления будет 13.678, т.к. цифре 5 предшествует четная цифра 8 (округляем вниз). 2) Число 13.6795 после окгруления будет 13.680. т.к. цифре 5 предшествует нечетная чифра 9 (округляем вверх).Пример кода, описывающего эту ситуацию (HALF_EVEN):
DecimalFormat df = new DecimalFormat("0.000");
System.out.println(df.format(13.6785));//результат 13,678
System.out.println(df.format(13.6795));//результат 13,680
Если вас не устраивает такое округление, то можно переключиться на округление, более привычное нам - округление в большую сторону (HALF_UP):
DecimalFormat df = new DecimalFormat("0.000");
df.setRoundingMode(RoundingMode.HALF_UP);
System.out.println(df.format(13.6785));//результат 13,679
System.out.println(df.format(13.6795));//результат 13,680