Давно хотелось попробовать реализовать фильтр Блума (хотя я его называют фильтром Блюма).
Фильтр Блума - это вероятностная структура данных, позволяющая проверить принадлежность элемента к множеству. Данная структура может точно ответить на запрос об отсутствии элемента в множестве, но может ошибаться с заданной нами вероятностью о наличии элемента во множестве.
В некоторых задачах фильтр Блума очень полезен, позволяет хранить меньше данных в оперативной памяти, позволяет снизить кол-во обращений к диску или другому оберегаемому ресурсу.
Фильтр Блума может использоваться, например, для подсчета уникальных посетителей, для проверки орфографии, в различных СУБД для уменьшения обращения к ПЗУ (постоянное запоминающее устройство).
Будем пробовать фильтр Блума на примере хранения 20 миллионов ИИНов.
ИИН - индивидуальный идентификационный номер физического лица в Республике Казахстан, состоящий из 12 цифр.
Я заранее сгенерировал список из 20 миллионов ИИНов (102 MB).
Скачать список можно здесь: https://drive.google.com/file/d/1SIfp_CRl4cQetc3Kw2jqDcWpF3fYPc2s/view?usp=sharing
Исходные коды генератора можно посмотреть в github: https://github.com/Nyquest/iin_generator
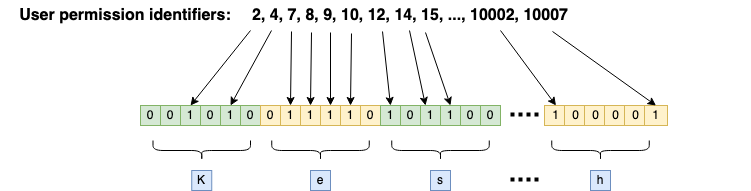
Фильтр Блума должен преобразовать наше множество из 20 миллионов ИИН в набор битов с помощью нескольких хэш-функций.
ИИН считается принадлежащим множеству, если значения всех вычисленных хэш-функции от ИИНа указывают на номера отмеченных бит. Если хотя бы один бит не отмечен, ИИН однозначно не принадлежит множеству.
Формулы
Оптимальное количество бит и достаточное кол-во хэш-функций можно рассчитать по формулам.
Формула оптимального количества бит:
![Rendered by QuickLaTeX.com \[ \displaystyle m=-{\frac {n\ln \varepsilon }{(\ln 2)^{2}}} \]](https://kesh.kz/blog/wp-content/ql-cache/quicklatex.com-123886bab26f262c82235268cfcca5f5_l3.png)
m - искомый размер битового массива (кол-во бит);
n - размер исходного множества;
ln - функция натурального логарифма;
ε - желаемая вероятность ошибок (например, 0.01 - ожидаем 1% ошибок)
Формула достаточного кол-ва кэш-функций зависит от выделенного кол-ва бит:
![Rendered by QuickLaTeX.com \[ \displaystyle k={\frac {m}{n}}\ln 2 \]](https://kesh.kz/blog/wp-content/ql-cache/quicklatex.com-1d72e2bd746b2315a4672efc067bdbad_l3.png)
k - кол-во кэш-функций;
m - кол-во битов в результирующем массиве;
n - кол-во элементов в исходном множестве;
ln - функция натурального логарифма.
Результатом выполнения каждой кэш-функции является номер бита, который нужно выставить (отметить). Таким образом, несколько хэш-функции высталяют различные биты в массиве бит. Хотя номера могут случайно совпадать для различных хэш-функций. Независимость хэш-функции друг от друга позволяет уменьшить повторяемость их результатов.
Реализация формул на Java
Самой главной проблемой при реализации фильтра Блума является выбор хэш-функций.
Первое, что пришло в голову это брать SHA-256 (привет любителям блокчейна) от ИИНа, и части SHA-256 использовать как отдельные значения хэш-функций.
Но, на самом деле, SHA-256 недостаточно, поэтому был взят SHA-384.
Чтобы было удобнее брать части SHA-384 делается выравнивание размера битового массива.
Как и требуется, хэши SHA обладают лавинным эффектом, небольшое изменений в хэшируемых данных меняет хэш до неузнаваемости.

Общая схема работы
Функция расчета оптимального кол-во бит
/**
* Вычислить оптимальное кол-во бит
* @param totalCount общее кол-во элементов
* @param errorProbability вероятность ошибок
* @return оптимальное кол-во бит
*/
static long optimalBitCount(long totalCount, double errorProbability) {
return (long) Math.ceil(
-totalCount * Math.log(errorProbability) / Math.pow(Math.log(2), 2));
}
Подставим наши значения (20 миллионов - кол-во элементов, 0.01 - ожидаем 1% ошибок) и получим размер битового массива, равный 191 701 168:
System.out.println(optimalBitCount(20_000_000, 0.01)); // 191_701_168
Но, именно для нашей реализации, данный размер не подходит, так как не все биты используются.
Это можно увидеть, переведя размер 191 701 168 в двоичный вид 1011011011010010000010110000:
System.out.println(Long.toBinaryString(optimalBitCount(20_000_000, 0.01)));
Чтобы задействовать возможные биты, нужно сделать расчет размера с выравниванием:
/**
* Вычислить оптимальное кол-во бит с выравниванием
* @param totalCount общее кол-во элементов
* @param errorProbability вероятность ошибок
* @return оптимальное кол-во бит в порции с выравниванием
*/
static long optimalBitCountWithAlignment(long totalCount, double errorProbability) {
long result = optimalBitCount(totalCount, errorProbability);
long l = Long.highestOneBit(result);
return l == totalCount ? totalCount : l << 1;
}
Еще раз подставим наши значения, получим размер, равный 268 435 456
System.out.println(optimalBitCountWithAlignment(20_000_000, 0.01)); // 268_435_456
Переведем 268 435 456 - 1 в двойчный вид 1111111111111111111111111111 (28 бит).
От размера массива нужно вычесть единицу, так как индексация массива идет с 0 и нужно посмотреть битовое представление последнего индекса.
System.out.println(Long.toBinaryString(
optimalBitCountWithAlignment(20_000_000, 0.01) - 1));
Размер стал больше, но зато все биты задействованы.
Таким образом, считаем размер битового массива равным 268 435 456.
Функция расчета кол-ва хэш-функций:
/**
* Расчет кол-ва хэш-функций
* @param totalCount общее кол-во элементов
* @param bitArraySize размер битового массив
* @return минимальное кол-во хэш-функций
*/
static long hashFunctionCount(long totalCount, long bitArraySize) {
return (long) Math.ceil(Math.log(2) * ((double)bitArraySize / totalCount));
}
Подставим наши значения, получим 10 хэш-функций:
System.out.println(hashFunctionCount(20_000_000, 268_435_456)); // 10
268 435 456 значений можно закодировать 28 битами, что составляет 3.5 байта.
![Rendered by QuickLaTeX.com \[ \displaystyle 2^{28} = 268 435 456 \]](https://kesh.kz/blog/wp-content/ql-cache/quicklatex.com-603be325d965336fca8ac772577100a8_l3.png)
Для удобства мы можем брать по 4 байта хэш-функции SHA, при этом 3 байта целиком, а один только на половину, другую же половину просто игнорируем.
Итого там потребуется 40 байт, которые есть в SHA-384.
| Хэш-функция | Кол-во бит | Кол-во байт
|
|---|
| SHA-256 | 256 | 32
|
| SHA-384 | 384 | 48
|
Из SHA-384 можно получить не 10, а 12 функций. Чем больше функций, тем меньше будет ошибок.
Реализация фильтра Блума на Java
Все необходимые расчеты сделаны, можно приступать к реализации.
Для начала реализуем получение хэша от строки (ИИНа) в виде массива байт.
MessageDigest digest = MessageDigest.getInstance("SHA-384");
byte[] digest(String value) {
return this.digest.digest(value.getBytes(StandardCharsets.UTF_8));
}
Биты будем хранить в стандартной структуре данных BitSet. У данный структуры есть методы set и get для установки и чтения значения соответствующего бита.
BitSet bitSet = new BitSet(1 << 28); // размер BitSet, равный 268_435_456
Реализуем функцию перевода четырех байт в число, являющееся номером позиции бита в BitSet.
/**
* переводим четыре байта в число
* @param digest массив байт
* @param position позиция, от которой берутся 4 байта
* @return число
*/
private int bitsToInt(byte[] digest, int position) {
return ((((1 << 4) - 1)) & digest[position]) << 24 // берем половину байта и смещаем его на 24 позиции влево
| (0xff & digest[position + 1]) << 16 // берем следующий целый байт и смещаем его на 16 позиций влево
| (0xff & digest[position + 2]) << 8 // берем следующий целый байт и смещаем его на 8 позиций влево
| (0xff & digest[position + 3]); // берем следующий целый байт без каких-либо смещений
}
Функция установки битов выглядит следующим образом:
private void saveBits(String value) {
byte[] digest = digest(value);
for (int i = 0; i + 3 < digest.length; i += 4) {
bitSet.set(bitsToInt(digest, i));
}
}
Функция проверки принадлежности значения множеству:
private boolean checkBits(String value) {
byte[] digest = digest(value);
for (int i = 0; i + 3 < digest.length; i += 4) {
if(!bitSet.get(bitsToInt(digest, i))) {
return false;
}
}
return true;
}
Тестирование фильтра Блума
Пример применения фильтра Блума на 20 миллионах ИИН https://github.com/Nyquest/bloom_filter
Проверять фильтр Блума будем следующим образом:
- Загрузим ИИНы в HashSet;
- Загрузим ИИНы в фильтр Блума;
- Сгенерим 10 миллионов случайных ИИН и прогоним их через фильтр Блума;
- Если фильтр показывает, что ИИН не относится к множеству, но этот ИИН есть в HashSet, то выбрасываем исключение и останавливаем программу;
- Если фильтр показывает, что ИИН относится к множеству, но его нет в HashSet, учитываем данный факт как ложноположительное срабатывание;
- Подсчитываем ложноположительные срабатывания и их в процент от общего числа запросов.
В примере две реализации: собственная MyBloomFilter и GoogleBloomFilter(BloomFilter из guava).
При создании GoogleBloomFilter указывается вероятность ошибок, которая подтверждается эмпирическим путем.
Но так как наш фильтр модифицирован дважды, эмпирические данные показывают ошибки в 0.18% от всех тестовых запросов:
- Набор бит увеличен из-за выравнивания
- Взято больше хэш-функций (12 вместо 10)
Теперь рассчитаем ожидаемую вероятность ошибок по формуле:
![Rendered by QuickLaTeX.com \[ \displaystyle (1-e^{-kn/m})^{k} \]](https://kesh.kz/blog/wp-content/ql-cache/quicklatex.com-2d01300f3b1433b54f3b2c2f6372a46b_l3.png)
Функция расчета вероятности ошибок на Java
/**
* Расчет вероятности ошибок
* @param totalCount общее кол-во элементов
* @param bitArraySize размер битового массив
* @param hashFunctionCount кол-во хэш-функций
* @return вероятность ошибок
*/
public static double errorProbability(long totalCount, long bitArraySize, long hashFunctionCount) {
return Math.pow(1 - Math.pow(Math.E,
-(double)hashFunctionCount * totalCount / bitArraySize), hashFunctionCount);
}
}
Подставим наши значения и получим 0.0018, т.е. теоретические и практические результаты совпали.
System.out.println(errorProbability(20_000_000, 268_435_456, 12));
Заключение
Получилась рабочая версия фильтра Блума, но с рядом недостатков.
Сравнивать будет с реализацией от Google, хотя почему-то в guava Bloom Filter еще в beta-тестировании.
Сравнение, конечно же, не в нашу пользу.
- Потребляет больше оперативной памяти из-за выравнивания;
- Непараметризирован. Размер битового массива фиксирован под определенную задачу.
- Сильная завязка на выравнивание.
- Реализация медленнее. С тестовым заданием фильтр в последовательном режиме справляется за 11 секунд, а GoogleBloomFilter за 5 секунд.
- Сама реализация как и BitSet без потоковой безопасности (thread-safety), в отличие от Guava Bloom Filter.
В реальных проектах лучше использовать готовые реализации Bloom Filter с потоковой безопасностью.
Основная цель своей реализации была лучше разобраться в этой интересной, вероятностной и магической структуре данных.
В реализации Google используется магия и трюки (см. фрагмент кода BloomFilterStrategies.java по добавлению элемента в множество):
@Override
public boolean put(
@ParametricNullness T object,
Funnel funnel,
int numHashFunctions,
LockFreeBitArray bits) {
long bitSize = bits.bitSize();
long hash64 = Hashing.murmur3_128().hashObject(object, funnel).asLong();
int hash1 = (int) hash64;
int hash2 = (int) (hash64 >>> 32);
boolean bitsChanged = false;
for (int i = 1; i <= numHashFunctions; i++) {
int combinedHash = hash1 + (i * hash2);
// Flip all the bits if it's negative (guaranteed positive number)
if (combinedHash < 0) {
combinedHash = ~combinedHash;
}
bitsChanged |= bits.set(combinedHash % bitSize);
}
return bitsChanged;
}
Здесь один хэш получается из предыдущего. Если в вычислениях случается переполнение, в результате которого образумется отрицательное число, то происходит инверсия бит, чтобы получилось положительное число за счет смены бита, отвечающего за знак в том числе. Чтобы не выходить за пределы битового массива делается закольцовывание с помощью взятия остатка от деления на размер массива.
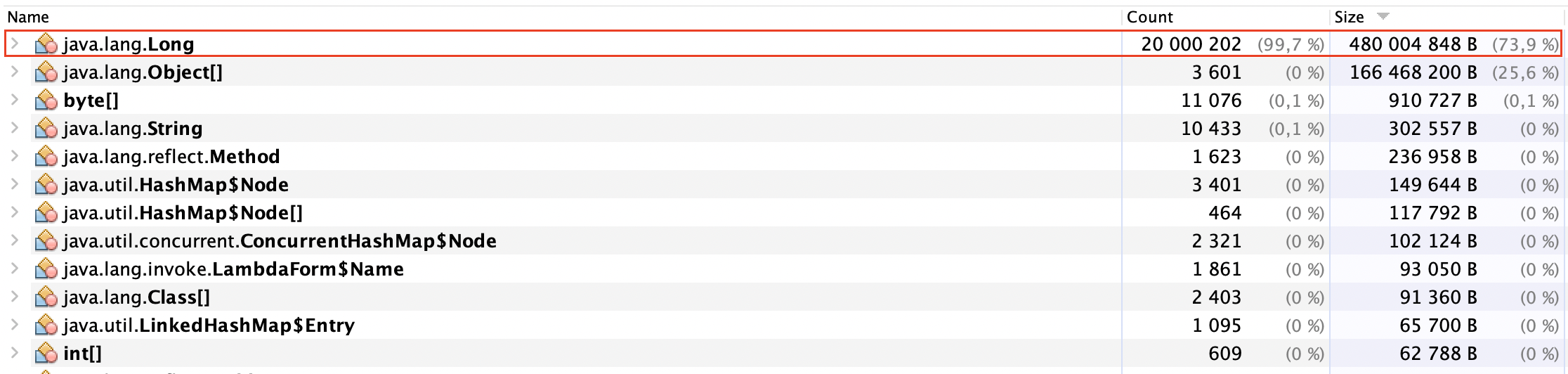
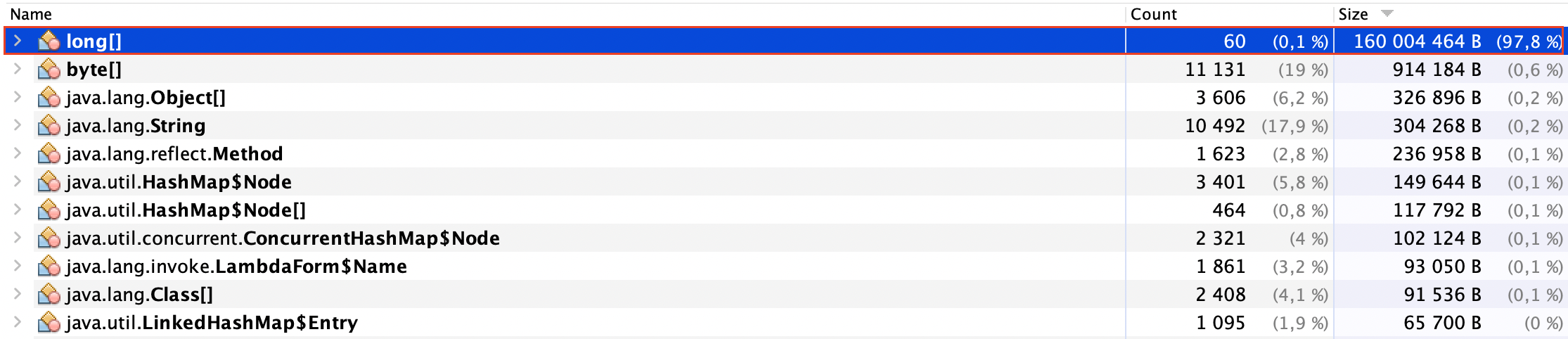
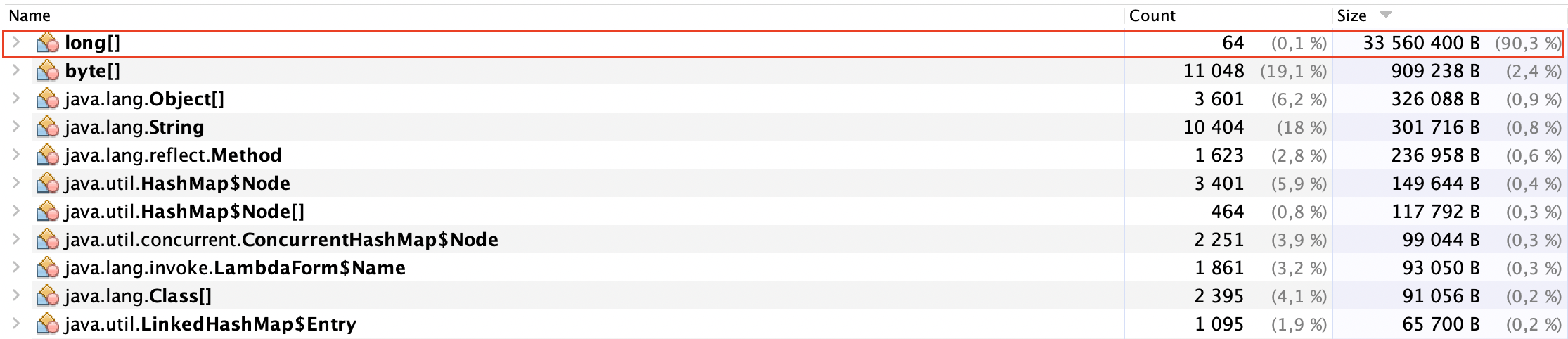
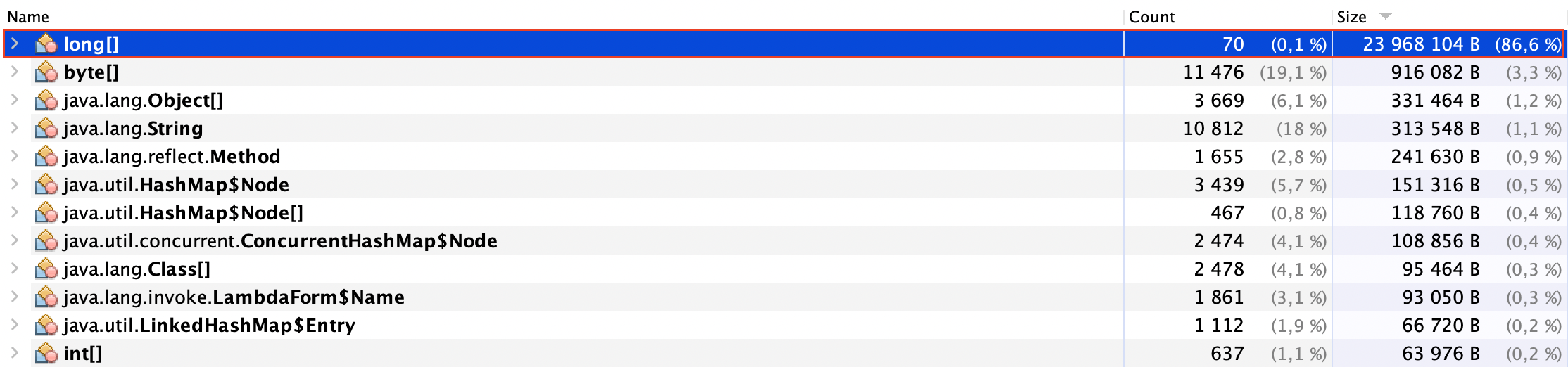
В следующем блоге смотрите эффективность фильтра Блума с точки зрения расхода памяти:
Эффективность фильтра Блума в памяти