Author Archive
Выгрузка простых чисел
Простые числа длины 1
Простые числа длины 2
Простые числа длины 3
Простые числа длины 4
Простые числа длины 5
Простые числа длины 6
Простые числа длины 7 (первые 10 тысяч чисел)
Простые числа длины 8 (первые 10 тысяч чисел)
Простые числа длины 9 (первые 10 тысяч чисел)
Сортировка по убыванию в Java
На данный момент, к сожалению, в Java нет стандартной функции, которая бы могла сортировать массив из примитивных элементов (например, int[], long[]) по убыванию.
Мы можем сортировать массив примитивов только по возрастанию:
int a[] = {17,4,85};
Arrays.sort(a);
System.out.println(Arrays.toString(a));//[4, 17, 85]
Как выход можно перевести массив примитивов в массив объектов (например, Integer[], Long[], String[]) и сортировать уже его:
Integer a[] = {17,4,85};
Arrays.sort(a,Collections.reverseOrder());
System.out.println(Arrays.toString(a));//[85, 17, 4]
Т.е. вторым параметром функции sort мы передали Collections.reverseOrder(), что обеспечило обратную сортировку.
Викторина на 8 марта
На 8 марта в нашей IT-компании решили одним из конкурсов сделать викторину, порыскав в интернете, я составил 20 вопросов:
- Самая древняя профессия
Ответ: Показать ответ
- У человека на двух руках 10 пальцев! Сколько пальцев на 10-ти руках?
Ответ: Показать ответ
- Назовите три русский женских имени не заканчивающихся ни на А, ни на Я
Ответ: Показать ответ
- Как звали первого программиста?
Ответ: Показать ответ
- Кто ходит сидя?
Ответ: Показать ответ
- Чего нет в женской сумочке?
Ответ: Показать ответ
- Что можно приготовить, но съесть нельзя?
Ответ: Показать ответ
- Что получиться если объединить Microsoft и iPhone?
Ответ: Показать ответ
- Какое колесо не крутится при правом развороте?
Ответ: Показать ответ
- Что не войдет в самую большую кастрюлю?
Ответ: Показать ответ
- А и Б сидели на трубе. А уехал за границу, Б чихнул и лёг в больницу. Что осталось на трубе?
Ответ: Показать ответ
- Винни-пух — поросёнок или кабан?
Ответ: Показать ответ
- Сколько грамм весит снаряженный пистолет Макарова:
Ответ: Показать ответ
- Что такое мультифора?
Ответ: Показать ответ
- Что такое "Паста ГОИ"
Ответ: Показать ответ
- Что такое "Метчик" и "Лерка"
Ответ: Показать ответ
- Планета супермена
Ответ: Показать ответ
- Седьмая планета от Солнца
Ответ: Показать ответ
- Самое большое озеро на Земле
Ответ: Показать ответ
- Назовите максимально длинное слово, в котором не повторяется ни одна буква
Ответ: Показать ответ
Генерация Java-классов Web-сервиса по WSDL
Допустим, у вас есть WSDL и вы хотите написать либо сам веб-сервис, либо клиента для сервиса. Для этого по WSDL нужно сгенерировать Java-классы с помощью утилиты wsimport, входящую в состав JDK.
Стоит отметить, что сгенерированный код может использовать и на сервере, и на клиенте.
Создайте новую папку и положите в нее вашу WSDL и всё, что к ней относится (это может быть другие WSDL или XSD). Увидеть все, что импортирует ваша основная WSDL можно в теге import. Например:
В данном примере следует заменить интернет адрес XSD на локальный:
Разумеется, файл example.xsd должен лежать c WSDL в одной директории.
Теперь напишем скрипт для генерирования классов. Рассмотрим сперва Windows-версию скрипта, а потом Linux-версию.
Скрипт для Windows
Создайте файл w-gen.bat в любом текстовом редакторе и скопируйте в него следующий код:
cls
set GEN_DIR=kz
rmdir %GEN_DIR% /s/q
"%JAVA_HOME%/bin/wsimport" -keep -Xnocompile -p kz.kesh.blog.v1 myBlog.wsdl
pause
cls - очистка консоли
GEN_DIR - директория пакета верхнего уровня
rmdir - полное удаление директории
wsimport - утилита для генерации Java-классов из WSDL
keep - сохраняет сгенерированные файлы
Xnocompile - не компилирует сгенерированные Java-файлы
kz.kesh.blog.v1 - имя пакета, в котором будет сгенерированые классы
myBlog.wsdl - наша WSDL
pause - пауза, чтобы консольное окно сразу не закрылось
Данный скрипт генерирует *.java файлы, но вы можете немного переработать скрипт и генерировать скопилированные файлы *.class. Так же вы можете доработать упаковку файлов и WSDL в jar. Например:
"%JAVA_HOME%/bin/jar" cf keskBlog.jar kz
jar - стандартная утилита из JDK для создания jar-файлов
cf - создает новый архив с указанным именем
keskBlog.jar - имя вашего jar-файла
kz - директория, которая упаковывается в jar, она соответствует названию верхнего пакета
Скрипт для Linux
Создайте файл w-gen.sh:
#!/bin/bash
GEN_DIR="kz"
rm -r $GEN_DIR
wsimport -keep -Xnocompile -p kz.kesh.blog.v1 myBlog.wsdl
Не забудьте дать скрипту права на выполенение:
chmod +x w-gen.sh
#!/bin/bash - обязательная строчка для bash-скриптов
GEN_DIR - директория пакета верхнего уровня
rm - рекурсивное удаление директории
wsimport - утилита для генерации Java-классов из WSDL
keep - сохраняет сгенерированные файлы
Xnocompile - не компилирует сгенерированные Java-файлы
kz.kesh.blog.v1 - имя пакета, в котором будет сгенерированы классы
myBlog.wsdl - наша WSDL
Установка CyanogenMod 11 на HTC One X
Это был мой первый опыт по установке неродной прошивки, поэтому я наступил на много граблей. Данная статья призвана помочь вам не допустить моих ошибок...
Два совета, которые позволят прошить CyanogenMod без лишних проблем и реанимации "кирпича":
 Причем, чтобы добраться до батерии, нужно разобрать - всё.
Передернув провод, я собрал аппарат. Боялся, что мог забыть подключить какой-нибудь шлейф (но в конце выясниться, что собрал девайс верно).
Аппарат по прежнему не включался, потом вычитал, что можно поключая, а потом отключая USB-кабель можно немного зарядить телефон. В итоге у меня включился телефон. И я понял, что разбирать телефон было не нужно!
Далее необходимо хорошо зарядить телефон, для этого я запускал вечно выполняющийся скрипт charge.bat.
Вот код этого скрипта:
Причем, чтобы добраться до батерии, нужно разобрать - всё.
Передернув провод, я собрал аппарат. Боялся, что мог забыть подключить какой-нибудь шлейф (но в конце выясниться, что собрал девайс верно).
Аппарат по прежнему не включался, потом вычитал, что можно поключая, а потом отключая USB-кабель можно немного зарядить телефон. В итоге у меня включился телефон. И я понял, что разбирать телефон было не нужно!
Далее необходимо хорошо зарядить телефон, для этого я запускал вечно выполняющийся скрипт charge.bat.
Вот код этого скрипта:
- Зарядите телефон на 100%
- Обязательно обновите HBOOT до версии 1.36.0000 или чуть выше
 Причем, чтобы добраться до батерии, нужно разобрать - всё.
Передернув провод, я собрал аппарат. Боялся, что мог забыть подключить какой-нибудь шлейф (но в конце выясниться, что собрал девайс верно).
Аппарат по прежнему не включался, потом вычитал, что можно поключая, а потом отключая USB-кабель можно немного зарядить телефон. В итоге у меня включился телефон. И я понял, что разбирать телефон было не нужно!
Далее необходимо хорошо зарядить телефон, для этого я запускал вечно выполняющийся скрипт charge.bat.
Вот код этого скрипта:
Причем, чтобы добраться до батерии, нужно разобрать - всё.
Передернув провод, я собрал аппарат. Боялся, что мог забыть подключить какой-нибудь шлейф (но в конце выясниться, что собрал девайс верно).
Аппарат по прежнему не включался, потом вычитал, что можно поключая, а потом отключая USB-кабель можно немного зарядить телефон. В итоге у меня включился телефон. И я понял, что разбирать телефон было не нужно!
Далее необходимо хорошо зарядить телефон, для этого я запускал вечно выполняющийся скрипт charge.bat.
Вот код этого скрипта:
@echo off
:start
fastboot getvar battery-voltage
fastboot reboot-bootloader
ping /n 6 localhost >nul
goto start
Скрипт все время с небольшой задержкой перегружает устройство, тем самым оно по чуть-чуть заряжается.
Вложенный тернарный поиск с золотым сечением
Определение тернарного поиска можно найти в Википедии. Также описание алгоритма можно найти здесь.
Реализация у тернарного поиска несложная, давайте убедимся в этом на примере следующей задачи:
Хотя данную задачу можно решать другими способами, но для учебных целей решим ее тернарным поиском.
Для начала нужно убедиться, что эту задачу вообще можно решить тернарным поиском. Убедимся в унимодальности нашей функции, т.е. на заданном интервале у функции должен быть один экстремум (максимальное или минимальное значение функции на заданном интервале).
Мы будем перебирать углы от 0° до 90°, т.е. наш интервал поиска от 0 до 90. При возрастании угла, начиная от 0°, площадь треугольника строго возрастает, затем при приближении к углу 90° площадь треугольнига строго уменьшается, т.е. у нас есть максимальное значение функции на данном интервале, а значит выполняется унимодальность функции, и мы можем применить тернарный поиск.
Как работает тернарный поиск.
Сначала интервал разбивается на три части, отсюда и название "тернарный" (Ternary переводится как тройной или троичный). На следующем шаге отсеивается участок, в котором точно нет решения, затем снова отрезок разбивается на три части, и это повторяется до тех пор, пока не будет достугнута необходимая точность результата.
Классический способ разбиения - это разбиение на три равные части части:
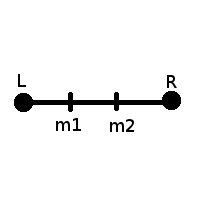 Фрагмент кода, обеспечивающий равенство отрезков Lm1 = m1m2 = m2R:
Фрагмент кода, обеспечивающий равенство отрезков Lm1 = m1m2 = m2R:
 2) Если f(m1) > f(m2), аналогично имеется только два случая, когда максимальное значение лежит в центральной или левой части, а значит правую часть можно отбросить.
2) Если f(m1) > f(m2), аналогично имеется только два случая, когда максимальное значение лежит в центральной или левой части, а значит правую часть можно отбросить.
 3) Если f(m1) = f(m2), то возможен только один вариант, при котором максимальное значение находится в центральной части, а значит левую и правую части можно отбросить.
3) Если f(m1) = f(m2), то возможен только один вариант, при котором максимальное значение находится в центральной части, а значит левую и правую части можно отбросить.
 Последний вариант, когда f(m1) = f(m2), в целях облегчения алгоритма можно заменить либо на этот случай f(m1) < f(m2), либо на этот f(m1) > f(m2). В скорости из-за этого, конечно же, мы чуть-чуть проиграем, но выиграем в скорости реализации алгоритма и компактности кода.
После каждого шага алгоритма от исходной области поиска остается 2/3, т.е. не самая большая скорость сходимости. Можно повысить скорость сходимости, если выбирать точки m1 и m2 ближе друг другу, правда при этом теряется точность. Повышение скорости сходимости может потребоваться в случае, когда вычисление функции f(x) занимает много времени и нужно минимизировать кол-во вызовов этой функции.
Очень хорошо при выборе точек m1 и m2 воспользоваться пропорциями золотого сечения. Если тернарный поиск использует пропорции золотого сечения, то это один в один Метод золотого сечения.
Последний вариант, когда f(m1) = f(m2), в целях облегчения алгоритма можно заменить либо на этот случай f(m1) < f(m2), либо на этот f(m1) > f(m2). В скорости из-за этого, конечно же, мы чуть-чуть проиграем, но выиграем в скорости реализации алгоритма и компактности кода.
После каждого шага алгоритма от исходной области поиска остается 2/3, т.е. не самая большая скорость сходимости. Можно повысить скорость сходимости, если выбирать точки m1 и m2 ближе друг другу, правда при этом теряется точность. Повышение скорости сходимости может потребоваться в случае, когда вычисление функции f(x) занимает много времени и нужно минимизировать кол-во вызовов этой функции.
Очень хорошо при выборе точек m1 и m2 воспользоваться пропорциями золотого сечения. Если тернарный поиск использует пропорции золотого сечения, то это один в один Метод золотого сечения.
Золотое сечение - это такое разбиение целого на две части, при котором отношение большего к меньшему равно отношению целого к большему
Это отношение постоянно и равно примерно 1,618, обозначается как φ и называется золотым числом: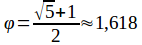 Для вычисления точек m1 и m2, разбивающих область поиска золотым сечением, воспользуемся следующими формулами:
Для вычисления точек m1 и m2, разбивающих область поиска золотым сечением, воспользуемся следующими формулами:
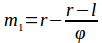
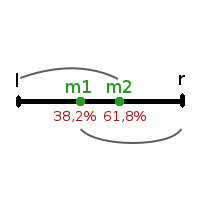
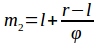 В процентном соотношении длины отрезков lm1 и lm2 приблизительно равны 38,2% и 61,8% от длины отрезка lr.
Благодаря свойствам золотого сечения точка m1 делит отрезок lm2 в пропорциях золотого сечения, а точка m2 делит отрезок m1r также в пропорциях золотого сечения.
В процентном соотношении длины отрезков lm1 и lm2 приблизительно равны 38,2% и 61,8% от длины отрезка lr.
Благодаря свойствам золотого сечения точка m1 делит отрезок lm2 в пропорциях золотого сечения, а точка m2 делит отрезок m1r также в пропорциях золотого сечения.
 И так мы видим, что сходимость золотого сечения будет 0,618, что лучше сходимости в случае разбиения области поиска на равные части, где сходимость у нас была 2/3 (0,66).
А теперь вернемся к решению задачи... Исходный код решения задачи на Java:
И так мы видим, что сходимость золотого сечения будет 0,618, что лучше сходимости в случае разбиения области поиска на равные части, где сходимость у нас была 2/3 (0,66).
А теперь вернемся к решению задачи... Исходный код решения задачи на Java:
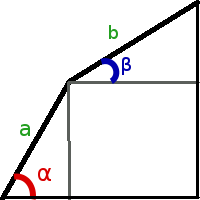 Сперва мы находим углы α1 и α2, которые разбивают область поиска на три равные части (в данной задачи можно не использовать золотое сечение). Далее для угла α1 с помощью вложенного тернарного поиска ищем угол β1, при котором площадь фигуры максимальна, аналогично, для угла α2 находим подходящий угол β2.
Сперва мы находим углы α1 и α2, которые разбивают область поиска на три равные части (в данной задачи можно не использовать золотое сечение). Далее для угла α1 с помощью вложенного тернарного поиска ищем угол β1, при котором площадь фигуры максимальна, аналогично, для угла α2 находим подходящий угол β2.
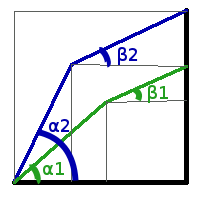 Найдя пары углов α1 и β1; α2 и β2, вычисляем площадь S1 и S2 соответственно. Можно использовать следующую формулу вычисления площади, где a и b - длины палок:
Найдя пары углов α1 и β1; α2 и β2, вычисляем площадь S1 и S2 соответственно. Можно использовать следующую формулу вычисления площади, где a и b - длины палок:
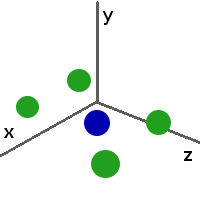 По условию задачи нам нужно вычислить координаты x,y,z строительства новой спасательной станции, причем расстояние от станции до самой дальней планеты должно быть минимально.
Сперва пробуем подобрать координату x тернарным поиском, но координаты y и z - неизвестны, поэтому зафиксировав некоторые точки x, полученные золотым сечением, мы запускаем вложенные тернарный поиск с фиксированной координатой x для поиска координаты y. Далее внутри поиска y запускаем вложенный тернарный поиск координаты z. Когда мы имеем все три зафиксированные координаты мы можем посчитать расстояния до всех планет и из них определить максимальное расстояние, это расстояние и будет значением функции f(x,y,z).
Т.к. в условии сказано, что количество планет может быть 100, то вычисление функции f(x,y,z) очень затратно по времени. Чтобы программа уложилась во временные рамки, нужно при тернарном поиске разбивать область поиска золотым сечением, а не на равные части. Тем самым у нас повыситься сходимость, т.е. вызовов функции f(x,y,z) станет меньше. Но при золотом сечении теряется точность, поэтому мы увеличим точность с 10-6 до 10-7.
Реализация на Java:
По условию задачи нам нужно вычислить координаты x,y,z строительства новой спасательной станции, причем расстояние от станции до самой дальней планеты должно быть минимально.
Сперва пробуем подобрать координату x тернарным поиском, но координаты y и z - неизвестны, поэтому зафиксировав некоторые точки x, полученные золотым сечением, мы запускаем вложенные тернарный поиск с фиксированной координатой x для поиска координаты y. Далее внутри поиска y запускаем вложенный тернарный поиск координаты z. Когда мы имеем все три зафиксированные координаты мы можем посчитать расстояния до всех планет и из них определить максимальное расстояние, это расстояние и будет значением функции f(x,y,z).
Т.к. в условии сказано, что количество планет может быть 100, то вычисление функции f(x,y,z) очень затратно по времени. Чтобы программа уложилась во временные рамки, нужно при тернарном поиске разбивать область поиска золотым сечением, а не на равные части. Тем самым у нас повыситься сходимость, т.е. вызовов функции f(x,y,z) станет меньше. Но при золотом сечении теряется точность, поэтому мы увеличим точность с 10-6 до 10-7.
Реализация на Java:
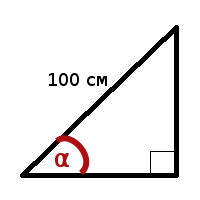
| Имеется прямоугольный треугольник, у которого гипотенуза равна 100 сантиметрам. Нужно вычислить при каком угле α площадь треугольника будет максимальна. |
 Фрагмент кода, обеспечивающий равенство отрезков Lm1 = m1m2 = m2R:
Фрагмент кода, обеспечивающий равенство отрезков Lm1 = m1m2 = m2R:
double m1 = l + (r - l) / 3;
double m2 = r - (r - l) / 3;
При сравнении значений функций в точках m1 и m2 у нас возможно три варианта:
1) Мы сдвигаем область поиска вправо, т.е. l становится равным m1 (l = m1);
2) Мы сдвигаем область поиска влево, т.е. r становится равным m2 (r = m2);
3) При равенстве значений функции в обеих точках, мы сдвигаем область поиска с обеих сторон, т.е. l становиться равным m1 (l = m1), а r становиться равным m2 (r = m2)
Рассмотрим данные случаи на примере поиска максимального значения.
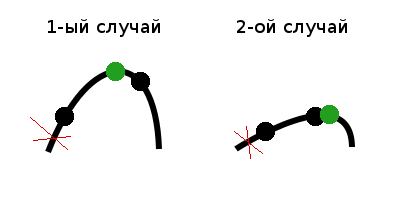
1) Если f(m1) < f(m2), возможно два случая: когда максимальное значение лежит в центральной части или в правой части, а значит левую часть можно отбросить. Максимальное значение обозначено зеленой точкой.
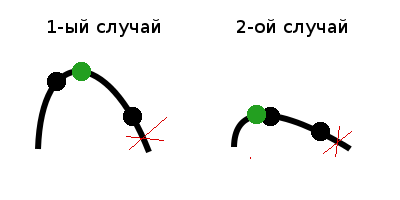
 2) Если f(m1) > f(m2), аналогично имеется только два случая, когда максимальное значение лежит в центральной или левой части, а значит правую часть можно отбросить.
2) Если f(m1) > f(m2), аналогично имеется только два случая, когда максимальное значение лежит в центральной или левой части, а значит правую часть можно отбросить.
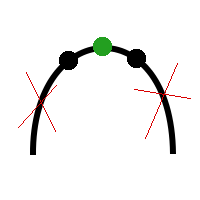
 3) Если f(m1) = f(m2), то возможен только один вариант, при котором максимальное значение находится в центральной части, а значит левую и правую части можно отбросить.
3) Если f(m1) = f(m2), то возможен только один вариант, при котором максимальное значение находится в центральной части, а значит левую и правую части можно отбросить.
 Последний вариант, когда f(m1) = f(m2), в целях облегчения алгоритма можно заменить либо на этот случай f(m1) < f(m2), либо на этот f(m1) > f(m2). В скорости из-за этого, конечно же, мы чуть-чуть проиграем, но выиграем в скорости реализации алгоритма и компактности кода.
После каждого шага алгоритма от исходной области поиска остается 2/3, т.е. не самая большая скорость сходимости. Можно повысить скорость сходимости, если выбирать точки m1 и m2 ближе друг другу, правда при этом теряется точность. Повышение скорости сходимости может потребоваться в случае, когда вычисление функции f(x) занимает много времени и нужно минимизировать кол-во вызовов этой функции.
Очень хорошо при выборе точек m1 и m2 воспользоваться пропорциями золотого сечения. Если тернарный поиск использует пропорции золотого сечения, то это один в один Метод золотого сечения.
Последний вариант, когда f(m1) = f(m2), в целях облегчения алгоритма можно заменить либо на этот случай f(m1) < f(m2), либо на этот f(m1) > f(m2). В скорости из-за этого, конечно же, мы чуть-чуть проиграем, но выиграем в скорости реализации алгоритма и компактности кода.
После каждого шага алгоритма от исходной области поиска остается 2/3, т.е. не самая большая скорость сходимости. Можно повысить скорость сходимости, если выбирать точки m1 и m2 ближе друг другу, правда при этом теряется точность. Повышение скорости сходимости может потребоваться в случае, когда вычисление функции f(x) занимает много времени и нужно минимизировать кол-во вызовов этой функции.
Очень хорошо при выборе точек m1 и m2 воспользоваться пропорциями золотого сечения. Если тернарный поиск использует пропорции золотого сечения, то это один в один Метод золотого сечения.
Золотое сечение - это такое разбиение целого на две части, при котором отношение большего к меньшему равно отношению целого к большему
Это отношение постоянно и равно примерно 1,618, обозначается как φ и называется золотым числом:
 И так мы видим, что сходимость золотого сечения будет 0,618, что лучше сходимости в случае разбиения области поиска на равные части, где сходимость у нас была 2/3 (0,66).
А теперь вернемся к решению задачи... Исходный код решения задачи на Java:
И так мы видим, что сходимость золотого сечения будет 0,618, что лучше сходимости в случае разбиения области поиска на равные части, где сходимость у нас была 2/3 (0,66).
А теперь вернемся к решению задачи... Исходный код решения задачи на Java:
import static java.lang.Math.*;
public class angle {
public static void main(String[] args) {
double l = 0;
double r = 90;
double EPS = 1e-6;//точность 0.000001
double hypo = 100;//гипотенуза
while(r - l >= EPS){//повторяем цикл пока не достигнем требуемой точности
double m1 = l + (r - l) / 3;
double m2 = r - (r - l) / 3;
if(f(hypo,m1) < f(hypo,m2)){
l = m1;
}else{
r = m2;
}
}
System.out.println((l + r) / 2);//результат 44.99999993498489
}
//функция расчета площади треугольника по гипотенузе и углу
static double f(double hypo,double alpha){
alpha = toRadians(alpha);
return 0.5 * hypo * hypo * cos(alpha) * sin(alpha);
}
}
Т.е. при угле в 44.999999° (45°) достигается максимальная площадь треугольника. В качестве ответа можно было взять значение из переменной l или r, это возможно благодаря достижению заданной точности результата, также можно взять их середину (l + r) / 2, как в рассмотренном выше коде.
Задача на вложенный тернарный поиск
В качестве примера применения вложенного тернарного поиска возьмем задачу "Футбольные ворота". С условием задачи можно ознакомиться здесь или здесь.
Найти максимальную площадь ворот можно, подобрав углы для палок α и β:
 Сперва мы находим углы α1 и α2, которые разбивают область поиска на три равные части (в данной задачи можно не использовать золотое сечение). Далее для угла α1 с помощью вложенного тернарного поиска ищем угол β1, при котором площадь фигуры максимальна, аналогично, для угла α2 находим подходящий угол β2.
Сперва мы находим углы α1 и α2, которые разбивают область поиска на три равные части (в данной задачи можно не использовать золотое сечение). Далее для угла α1 с помощью вложенного тернарного поиска ищем угол β1, при котором площадь фигуры максимальна, аналогично, для угла α2 находим подходящий угол β2.
 Найдя пары углов α1 и β1; α2 и β2, вычисляем площадь S1 и S2 соответственно. Можно использовать следующую формулу вычисления площади, где a и b - длины палок:
Найдя пары углов α1 и β1; α2 и β2, вычисляем площадь S1 и S2 соответственно. Можно использовать следующую формулу вычисления площади, где a и b - длины палок:
S = 0.5 * a * a * cos(alpha) * sin(alpha) + 0.5 * b * b * cos(beta) * sin(beta) + a * b * sin(alpha) * cos(beta)Сравнив полученные площади, мы можем отсеять треть диапазона углов, которые дают маленькую площадь. И повторяем эти шаги до тех пор, пока не достигнем требуемой точности. Код решения задачи на Java:
import java.io.*;
import static java.lang.Math.*;
import java.text.DecimalFormat;
import java.text.DecimalFormatSymbols;
import java.util.*;
public class FooballGate {
static int a;//длина 1-ой палки
static int b;//длина 2-ой палки
static double EPS = 1e-6;//точность результата
public static void main(String[] args) throws IOException {
Scanner s = new Scanner(new File("input.txt"));
s.useLocale(Locale.US);
a = s.nextInt();
b = s.nextInt();
s.close();
double l = 0;
double r = 90;
while(r - l >= EPS){
double m1 = l + (r - l) / 3;
double m2 = r - (r - l) / 3;
if(f(m1) < f(m2)){
l = m1;
}else{
r = m2;
}
}
double ans = f((l + r) / 2);//результат
DecimalFormat df = new DecimalFormat("0.00000000",
DecimalFormatSymbols.getInstance(Locale.US));
System.out.println(df.format(ans));//вывод с восемью знаками после запятой
}
//функция расчета площади с фиксированным углом alpha,
//в которой тернарным поиском идет поиск угла beta,
//при котором площадь максимальна
static double f(double alpha){
double l = 0;
double r = 90;
while(r - l >= EPS){
double m1 = l + (r - l) / 3;
double m2 = r - (r - l) / 3;
if(f(alpha,l) < f(alpha,r)){
l = m1;
}else{
r = m2;
}
}
return f(alpha,(l + r) / 2);
}
//функция расчета площади в зависимости от углов: alpha и beta
static double f(double alpha, double beta){
alpha = toRadians(alpha);
beta = toRadians(beta);
return 0.5 * a * a * cos(alpha) * sin(alpha) +
0.5 * b * b * cos(beta) * sin(beta) +
a * b * sin(alpha) * cos(beta);
}
}
Задача на тройную вложенность тернарного поиска с необходимостью применения золотого сечения
Задача называется "Космические спасатели". Ознакомиться с условием задачи можно здесь или здесь.
 По условию задачи нам нужно вычислить координаты x,y,z строительства новой спасательной станции, причем расстояние от станции до самой дальней планеты должно быть минимально.
Сперва пробуем подобрать координату x тернарным поиском, но координаты y и z - неизвестны, поэтому зафиксировав некоторые точки x, полученные золотым сечением, мы запускаем вложенные тернарный поиск с фиксированной координатой x для поиска координаты y. Далее внутри поиска y запускаем вложенный тернарный поиск координаты z. Когда мы имеем все три зафиксированные координаты мы можем посчитать расстояния до всех планет и из них определить максимальное расстояние, это расстояние и будет значением функции f(x,y,z).
Т.к. в условии сказано, что количество планет может быть 100, то вычисление функции f(x,y,z) очень затратно по времени. Чтобы программа уложилась во временные рамки, нужно при тернарном поиске разбивать область поиска золотым сечением, а не на равные части. Тем самым у нас повыситься сходимость, т.е. вызовов функции f(x,y,z) станет меньше. Но при золотом сечении теряется точность, поэтому мы увеличим точность с 10-6 до 10-7.
Реализация на Java:
По условию задачи нам нужно вычислить координаты x,y,z строительства новой спасательной станции, причем расстояние от станции до самой дальней планеты должно быть минимально.
Сперва пробуем подобрать координату x тернарным поиском, но координаты y и z - неизвестны, поэтому зафиксировав некоторые точки x, полученные золотым сечением, мы запускаем вложенные тернарный поиск с фиксированной координатой x для поиска координаты y. Далее внутри поиска y запускаем вложенный тернарный поиск координаты z. Когда мы имеем все три зафиксированные координаты мы можем посчитать расстояния до всех планет и из них определить максимальное расстояние, это расстояние и будет значением функции f(x,y,z).
Т.к. в условии сказано, что количество планет может быть 100, то вычисление функции f(x,y,z) очень затратно по времени. Чтобы программа уложилась во временные рамки, нужно при тернарном поиске разбивать область поиска золотым сечением, а не на равные части. Тем самым у нас повыситься сходимость, т.е. вызовов функции f(x,y,z) станет меньше. Но при золотом сечении теряется точность, поэтому мы увеличим точность с 10-6 до 10-7.
Реализация на Java:
import java.io.*;
import java.text.DecimalFormat;
import java.text.DecimalFormatSymbols;
import java.util.*;
public class SpaceRescuers {
static int MAX = (int) 1e4;//максимальная граница поиска
static int MIN = -MAX;//минимальная граница поиска
static class Point{
int x;
int y;
int z;
public Point(int x, int y, int z) {
super();
this.x = x;
this.y = y;
this.z = z;
}
}
static class PointD{
double x;
double y;
double z;
public PointD(double x, double y, double z) {
super();
this.x = x;
this.y = y;
this.z = z;
}
}
static Point[] points;
static double EPS = 1e-7;
static PointD bestPoint;//лучшая точка
static double best = Double.MAX_VALUE;//лучшее расстояние (минимальное)
static double fi = 1 / ((Math.sqrt(5) + 1) / 2);
public static void main(String[] args) throws IOException {
Scanner s = new Scanner(new File("input.txt"));
s.useLocale(Locale.US);
int N = s.nextInt();
points = new Point[N];
for(int i = 0; i < N; i++){
points[i] = new Point(s.nextInt(),s.nextInt(),s.nextInt());
}
s.close();
double l = MIN;
double r = MAX;
while(r - l > EPS){
double delta = (r - l) * fi;
double m1 = r - delta;
double m2 = l + delta;
if(f(m1) > f(m2)){
l = m1;
}else{
r = m2;
}
}
double x = bestPoint.x;
double y = bestPoint.y;
double z = bestPoint.z;
DecimalFormat df = new DecimalFormat("0.000000",
DecimalFormatSymbols.getInstance(Locale.US));
System.out.println(df.format(x) + " " + df.format(y) + " " +
df.format(z));
}
//опредение минимального расстояния при фиксированной координате x
static double f(double x){
double l = MIN;
double r = MAX;
while(r - l > EPS){
double delta = (r - l) * fi;
double m1 = r - delta;
double m2 = l + delta;
if(f(x,m1) > f(x,m2)){
l = m1;
}else{
r = m2;
}
}
return f(x,(l + r) / 2);
}
//определение минимального расстояния при фиксированных координатах x и y
static double f(double x,double y){
double l = MIN;
double r = MAX;
while(r - l > EPS){
double delta = (r - l) * fi;
double m1 = r - delta;
double m2 = l + delta;
if(f(x,y,m1) > f(x,y,m2)){
l = m1;
}else{
r = m2;
}
}
return f(x,y,(l + r) / 2);
}
//определение минимального расстояния при фиксированных координатах x,y и z
static double f(double x,double y,double z){
double max = 0;
for(int i = 0; i < points.length; i++){
Point p = points[i];
double s =
(p.x - x) * (p.x - x) +
(p.y - y) * (p.y - y) +
(p.z - z) * (p.z - z);
max = Math.max(max, s);
}
if(max < best){
best = max;
bestPoint = new PointD(x,y,z);
}
return max;
}
}
Обратите внимание на некоторые места в коде:
- Мы рассчитываем не φ, а 1/φ, чтобы дальше в вычислениях использовать умножение, а не деление, т.к. умножение работает быстрее;
static double fi = 1 / ((Math.sqrt(5) + 1) / 2);
double delta = (r - l) * fi; double m1 = r - delta; double m2 = l + delta;
- В первых двух задачах мы рассматривали поиск максимального значения, а данной задаче нас интересует минимально значение, поэтому в условном операторе меняется условие:
if(f(m1) > f(m2)){ l = m1; }else{ r = m2; } - Обратите внимание, что при расчете расстояния извлечение квадратного корня опущено.
double s = (p.x - x) * (p.x - x) + (p.y - y) * (p.y - y) + (p.z - z) * (p.z - z);
Извлечение квадратног корня - очень затратная операция. Сравнивать расстояния можно и без извлечения корня, а если бы потребовалось узнать самое минимальное расстояние, то корень можно было бы извлечь в самом конце.
Сортировка кучей (GCC 4.9.1)
Реализация на GCC 4.9.1 сортировки кучей (пирамидальная сортировка).
У сортировки кучей два больших достоинства:
- В худшем случае работает за O(n * log n)
- Не требует дополнительной памяти
#include
//получить индекс левого потомка
int left(int i){
return i * 2 + 1;
}
//получить индекс правого потомка
int right(int i){
return i * 2 + 2;
}
//поменять местами два элемента массива
int swap(int *a,int i,int j){
int tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
//вывести на экран массив
void print(int *a,int size){
int i;
for(i=0;i=0;i--){
heapify(a,size,i);
}
}
//сортировка кучей
void heapSort(int *a,int size){
buildHeap(a,size);
// printf("build\n");
// print(a,size);
while(--size > 0){
swap(a,0,size);
heapify(a,size,0);
}
}
int main(){
const int N = 9;
int arr[9] = {1,6,3,5,9,4,2,8,7};
print(arr,N);//вывести на экран исходный массив
heapSort(arr,N);//сортировка кучей
printf("=============\n");
print(arr,N);//вывод отсортированного массива
return 0;
}
В результате исходный массив (1 6 3 5 9 4 2 8 7) будет отсортирован (1 2 3 4 5 6 7 8 9). Баянаул 2014
Статья о том, как добраться с Астаны до Баянаула своим ходом и вернуться обратно.
Боровое уже наскучило, поэтому решили съездить в Баянаул.
Природа там ни чем не уступает боровому, но нас сразу предупредили, что ждать комфорта не стоит.
Решили поехать в будний день. Купили билеты на автобус через сайт http://saparzhai.kz на 11 августа до Экибастуза. Отправление автобуса было в 09:20 утра. Взрослый билет обошелся в 2000 тенге + 50 тенге комиссии.
Примерно через 5 часов мы оказались в незнакомом нам Экибастузе. Зашли на вокзал, чтобы узнать, когда будет автобус до Жасыбая. Да-да, именно до Жасыбая, а Баянаул находится по пути. Но речь не об этом, а о том, что автобус до Жасыбая ходит только утром. Мы хотели узнать: как еще можно добраться и где стоят таксисты. Но сотрудница, зная, что следующий автобус только утром, ничего не подсказала, сославшись на то, что такси не относится к вокзалу. В итоге пошли за территорию вокзала искать такси...
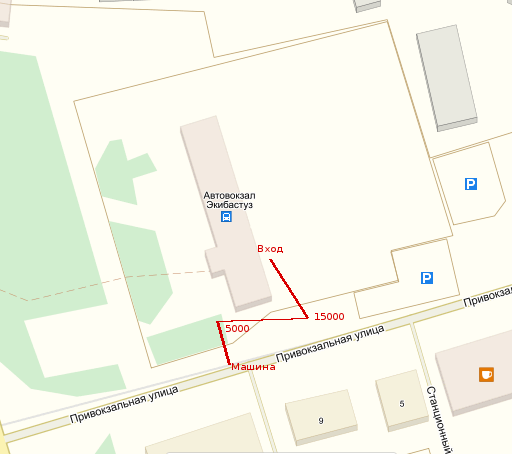 Выйдя с территории вокзал, сразу же стол таксёрик, который зарядил 15 тысяч тенге до Жасыбая.
Мы были в шоке... Потом решили пройти чуть дальше, там под деревом сидели два мужика-зазывалы. Они сказали по 2500 с каждого и сразу поедем. Это нас очень устроило. Нас проводили через дорогу, где нас передали другому таксисту. Но поехали мы не сразу, а немного подождали, пока наберется людей в машину. В итоге набралось нас - двое, парень и женщина. Так и поехали.
По дороге встречались угольные разрезы. Очень часто захватывало дух, но не из-за угольных разрезов, а из-за резких спусков после подъема, дорога вообще волнистая.
По пути заехали в Баянаул,оставили там женщин и поехали дальне в Жасыбай. Дальше была даже немного серпантинная дорога. Заранее мы не договаривались о месте нашей остановки, решили на месте осмотреться. Добравшись до Жасыбая, в первую очередь водитель отвез парня-попутчика в какую-то зону отдыха, окрашенную в розовые тона. Несмотря на будние дни, там было очень много людно, что не очень понравилось нам. Но до воды, т.к. озера было рукой подать. Решили не ехать туда, где планировали искать место остановки, а искать место у воды, чтобы выйти и сразу в воду. Водитель нам попался очень хороший (Баха - сын Аллаха, как он сам себя назвал), созвонился со знакомыми, узнать о наличии мест, и мы отправились в зону отдыха "Березовая роща".
Там нас встретили, проводили до женщины, которая показала номер. Вообще до это нас предупреждали, что не стоит ждать комфорта, и в тех зонах отдыха, что мы смотрели по интеренету туалет и душ были общими. А тут номер и в нем есть туалет и душ. Что очень порадовало. Номер обошелся в 9000 за сутки, мы взяли на два дня. Мы хотели посмотреть номера за 6000, но нам сказали, что они с подселением, и мы не стали смотреть, а оплатив 18 тыс. остались в этом номере. Номер был на первом этаже, в номере был телевизор, по-моему даже холодильник. Устроившись и переодевшись мы пошли на пляж. Как видно на картинке ниже - пляж недалеко:
Выйдя с территории вокзал, сразу же стол таксёрик, который зарядил 15 тысяч тенге до Жасыбая.
Мы были в шоке... Потом решили пройти чуть дальше, там под деревом сидели два мужика-зазывалы. Они сказали по 2500 с каждого и сразу поедем. Это нас очень устроило. Нас проводили через дорогу, где нас передали другому таксисту. Но поехали мы не сразу, а немного подождали, пока наберется людей в машину. В итоге набралось нас - двое, парень и женщина. Так и поехали.
По дороге встречались угольные разрезы. Очень часто захватывало дух, но не из-за угольных разрезов, а из-за резких спусков после подъема, дорога вообще волнистая.
По пути заехали в Баянаул,оставили там женщин и поехали дальне в Жасыбай. Дальше была даже немного серпантинная дорога. Заранее мы не договаривались о месте нашей остановки, решили на месте осмотреться. Добравшись до Жасыбая, в первую очередь водитель отвез парня-попутчика в какую-то зону отдыха, окрашенную в розовые тона. Несмотря на будние дни, там было очень много людно, что не очень понравилось нам. Но до воды, т.к. озера было рукой подать. Решили не ехать туда, где планировали искать место остановки, а искать место у воды, чтобы выйти и сразу в воду. Водитель нам попался очень хороший (Баха - сын Аллаха, как он сам себя назвал), созвонился со знакомыми, узнать о наличии мест, и мы отправились в зону отдыха "Березовая роща".
Там нас встретили, проводили до женщины, которая показала номер. Вообще до это нас предупреждали, что не стоит ждать комфорта, и в тех зонах отдыха, что мы смотрели по интеренету туалет и душ были общими. А тут номер и в нем есть туалет и душ. Что очень порадовало. Номер обошелся в 9000 за сутки, мы взяли на два дня. Мы хотели посмотреть номера за 6000, но нам сказали, что они с подселением, и мы не стали смотреть, а оплатив 18 тыс. остались в этом номере. Номер был на первом этаже, в номере был телевизор, по-моему даже холодильник. Устроившись и переодевшись мы пошли на пляж. Как видно на картинке ниже - пляж недалеко:
 Что касается магазинов: магазин на территории зоны отдыха есть, но пока мы там были, он всё время был закрыт. Пару раз мы сходили за водой до этих магазинчиков:
Что касается магазинов: магазин на территории зоны отдыха есть, но пока мы там были, он всё время был закрыт. Пару раз мы сходили за водой до этих магазинчиков:
 Но на следующий день мы нашли более короткий путь - по пляжу, но в одном месте нужно на корточках проползти под забором:
Но на следующий день мы нашли более короткий путь - по пляжу, но в одном месте нужно на корточках проползти под забором:
 Также мы не стали далеко идти в горы, а чисто символически сходили в ближайшие горы:
Также мы не стали далеко идти в горы, а чисто символически сходили в ближайшие горы:
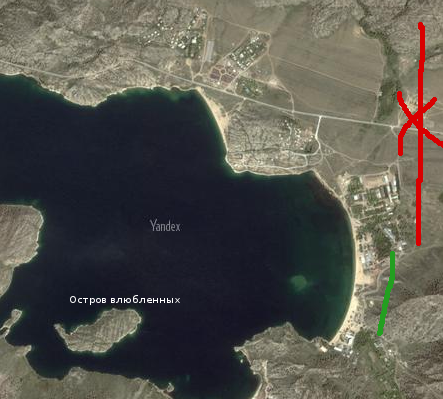 Вот такой вид там открывается:
Вот такой вид там открывается:
 Если смотреть с берега, то кажется, что озеро куда-то сворачивает за горы. Но с горы уже видно, что перед нами полуостров, это потом уже вернувшить в Астану, я увидел на карте, что это остров. И назвается этот остров - "Остров влюбленных". Если бы мы знали раньше, что это остров, то прокатились бы до острова на катамаранах. А вообще люди на катамаранах плыли не к острову, а чуть поближе, к месту, где было не так глубоко, что даже было видно с высоты желтоватую воду. Возможно, в этом месте из воды выступали камни. Стоит немного рассказать о воде. Вода чистая, берег песчанный, дно тебя не засасывает, как в Боровом. Нужно довольно далеко отойти от берега, чтобы стало глубоко. Нырять с разбегу - не советую, так как на дне лежат большие камни. Да и плавать нужно осторожно, чтобы не наплыть на камень. Местами встречаются водоросли, поэтому приходилось смотреть в воду и высматривать камни и водоросли.
Людей тут очень мало, кто любит уединение - здесь понравиться.
Питание. По пути на пляж у нас была столовая, в которой можно было позавтракать, пообедать и поужинать, но в строго определенные для этого время. На территории есть мангал, но мясо нужно привозить с собой. Чтобы покушать шашлык и попить пиво также нужно идти в сторону трассы.
Теперь о возвращении. В день отъезда позвонили Бахи, он нашел нам попутное такси. Выйдя за территорию и немного пождав, подъехала машина, в которой были уже два пассажира. Я спросил столько с нас возьмут, оказалось еще дешевле 2000 с человека, нас это очень даже устроило и мы поехали в Экибастуз. У нас был поезд, поэтому нас привезли на железнодорожный вокзал. Также мы проголодались, но неудобство небольших городов - это отсутствие мест, где можно покушать, т.к. все питаются дома. По крайней мере, мы не нашли возле вокзала нормального места покушать. В итоге решили пойти в сторону автовокзала и не ошиблись, через дорогу от автовокзала была кафешка, где мы пообедали. Далее вернулись на ж/д вокзал. Было очень тяжело в поезде, т.к. было очень нужно, в нашей секции плацкарта не открывалось окно :(.
Но не смотря на это, поездка удалась на славу 🙂
Если смотреть с берега, то кажется, что озеро куда-то сворачивает за горы. Но с горы уже видно, что перед нами полуостров, это потом уже вернувшить в Астану, я увидел на карте, что это остров. И назвается этот остров - "Остров влюбленных". Если бы мы знали раньше, что это остров, то прокатились бы до острова на катамаранах. А вообще люди на катамаранах плыли не к острову, а чуть поближе, к месту, где было не так глубоко, что даже было видно с высоты желтоватую воду. Возможно, в этом месте из воды выступали камни. Стоит немного рассказать о воде. Вода чистая, берег песчанный, дно тебя не засасывает, как в Боровом. Нужно довольно далеко отойти от берега, чтобы стало глубоко. Нырять с разбегу - не советую, так как на дне лежат большие камни. Да и плавать нужно осторожно, чтобы не наплыть на камень. Местами встречаются водоросли, поэтому приходилось смотреть в воду и высматривать камни и водоросли.
Людей тут очень мало, кто любит уединение - здесь понравиться.
Питание. По пути на пляж у нас была столовая, в которой можно было позавтракать, пообедать и поужинать, но в строго определенные для этого время. На территории есть мангал, но мясо нужно привозить с собой. Чтобы покушать шашлык и попить пиво также нужно идти в сторону трассы.
Теперь о возвращении. В день отъезда позвонили Бахи, он нашел нам попутное такси. Выйдя за территорию и немного пождав, подъехала машина, в которой были уже два пассажира. Я спросил столько с нас возьмут, оказалось еще дешевле 2000 с человека, нас это очень даже устроило и мы поехали в Экибастуз. У нас был поезд, поэтому нас привезли на железнодорожный вокзал. Также мы проголодались, но неудобство небольших городов - это отсутствие мест, где можно покушать, т.к. все питаются дома. По крайней мере, мы не нашли возле вокзала нормального места покушать. В итоге решили пойти в сторону автовокзала и не ошиблись, через дорогу от автовокзала была кафешка, где мы пообедали. Далее вернулись на ж/д вокзал. Было очень тяжело в поезде, т.к. было очень нужно, в нашей секции плацкарта не открывалось окно :(.
Но не смотря на это, поездка удалась на славу 🙂
 Выйдя с территории вокзал, сразу же стол таксёрик, который зарядил 15 тысяч тенге до Жасыбая.
Мы были в шоке... Потом решили пройти чуть дальше, там под деревом сидели два мужика-зазывалы. Они сказали по 2500 с каждого и сразу поедем. Это нас очень устроило. Нас проводили через дорогу, где нас передали другому таксисту. Но поехали мы не сразу, а немного подождали, пока наберется людей в машину. В итоге набралось нас - двое, парень и женщина. Так и поехали.
По дороге встречались угольные разрезы. Очень часто захватывало дух, но не из-за угольных разрезов, а из-за резких спусков после подъема, дорога вообще волнистая.
По пути заехали в Баянаул,оставили там женщин и поехали дальне в Жасыбай. Дальше была даже немного серпантинная дорога. Заранее мы не договаривались о месте нашей остановки, решили на месте осмотреться. Добравшись до Жасыбая, в первую очередь водитель отвез парня-попутчика в какую-то зону отдыха, окрашенную в розовые тона. Несмотря на будние дни, там было очень много людно, что не очень понравилось нам. Но до воды, т.к. озера было рукой подать. Решили не ехать туда, где планировали искать место остановки, а искать место у воды, чтобы выйти и сразу в воду. Водитель нам попался очень хороший (Баха - сын Аллаха, как он сам себя назвал), созвонился со знакомыми, узнать о наличии мест, и мы отправились в зону отдыха "Березовая роща".
Там нас встретили, проводили до женщины, которая показала номер. Вообще до это нас предупреждали, что не стоит ждать комфорта, и в тех зонах отдыха, что мы смотрели по интеренету туалет и душ были общими. А тут номер и в нем есть туалет и душ. Что очень порадовало. Номер обошелся в 9000 за сутки, мы взяли на два дня. Мы хотели посмотреть номера за 6000, но нам сказали, что они с подселением, и мы не стали смотреть, а оплатив 18 тыс. остались в этом номере. Номер был на первом этаже, в номере был телевизор, по-моему даже холодильник. Устроившись и переодевшись мы пошли на пляж. Как видно на картинке ниже - пляж недалеко:
Выйдя с территории вокзал, сразу же стол таксёрик, который зарядил 15 тысяч тенге до Жасыбая.
Мы были в шоке... Потом решили пройти чуть дальше, там под деревом сидели два мужика-зазывалы. Они сказали по 2500 с каждого и сразу поедем. Это нас очень устроило. Нас проводили через дорогу, где нас передали другому таксисту. Но поехали мы не сразу, а немного подождали, пока наберется людей в машину. В итоге набралось нас - двое, парень и женщина. Так и поехали.
По дороге встречались угольные разрезы. Очень часто захватывало дух, но не из-за угольных разрезов, а из-за резких спусков после подъема, дорога вообще волнистая.
По пути заехали в Баянаул,оставили там женщин и поехали дальне в Жасыбай. Дальше была даже немного серпантинная дорога. Заранее мы не договаривались о месте нашей остановки, решили на месте осмотреться. Добравшись до Жасыбая, в первую очередь водитель отвез парня-попутчика в какую-то зону отдыха, окрашенную в розовые тона. Несмотря на будние дни, там было очень много людно, что не очень понравилось нам. Но до воды, т.к. озера было рукой подать. Решили не ехать туда, где планировали искать место остановки, а искать место у воды, чтобы выйти и сразу в воду. Водитель нам попался очень хороший (Баха - сын Аллаха, как он сам себя назвал), созвонился со знакомыми, узнать о наличии мест, и мы отправились в зону отдыха "Березовая роща".
Там нас встретили, проводили до женщины, которая показала номер. Вообще до это нас предупреждали, что не стоит ждать комфорта, и в тех зонах отдыха, что мы смотрели по интеренету туалет и душ были общими. А тут номер и в нем есть туалет и душ. Что очень порадовало. Номер обошелся в 9000 за сутки, мы взяли на два дня. Мы хотели посмотреть номера за 6000, но нам сказали, что они с подселением, и мы не стали смотреть, а оплатив 18 тыс. остались в этом номере. Номер был на первом этаже, в номере был телевизор, по-моему даже холодильник. Устроившись и переодевшись мы пошли на пляж. Как видно на картинке ниже - пляж недалеко:
 Что касается магазинов: магазин на территории зоны отдыха есть, но пока мы там были, он всё время был закрыт. Пару раз мы сходили за водой до этих магазинчиков:
Что касается магазинов: магазин на территории зоны отдыха есть, но пока мы там были, он всё время был закрыт. Пару раз мы сходили за водой до этих магазинчиков:
 Но на следующий день мы нашли более короткий путь - по пляжу, но в одном месте нужно на корточках проползти под забором:
Но на следующий день мы нашли более короткий путь - по пляжу, но в одном месте нужно на корточках проползти под забором:
 Также мы не стали далеко идти в горы, а чисто символически сходили в ближайшие горы:
Также мы не стали далеко идти в горы, а чисто символически сходили в ближайшие горы:
 Вот такой вид там открывается:
Вот такой вид там открывается:
 Если смотреть с берега, то кажется, что озеро куда-то сворачивает за горы. Но с горы уже видно, что перед нами полуостров, это потом уже вернувшить в Астану, я увидел на карте, что это остров. И назвается этот остров - "Остров влюбленных". Если бы мы знали раньше, что это остров, то прокатились бы до острова на катамаранах. А вообще люди на катамаранах плыли не к острову, а чуть поближе, к месту, где было не так глубоко, что даже было видно с высоты желтоватую воду. Возможно, в этом месте из воды выступали камни. Стоит немного рассказать о воде. Вода чистая, берег песчанный, дно тебя не засасывает, как в Боровом. Нужно довольно далеко отойти от берега, чтобы стало глубоко. Нырять с разбегу - не советую, так как на дне лежат большие камни. Да и плавать нужно осторожно, чтобы не наплыть на камень. Местами встречаются водоросли, поэтому приходилось смотреть в воду и высматривать камни и водоросли.
Людей тут очень мало, кто любит уединение - здесь понравиться.
Питание. По пути на пляж у нас была столовая, в которой можно было позавтракать, пообедать и поужинать, но в строго определенные для этого время. На территории есть мангал, но мясо нужно привозить с собой. Чтобы покушать шашлык и попить пиво также нужно идти в сторону трассы.
Теперь о возвращении. В день отъезда позвонили Бахи, он нашел нам попутное такси. Выйдя за территорию и немного пождав, подъехала машина, в которой были уже два пассажира. Я спросил столько с нас возьмут, оказалось еще дешевле 2000 с человека, нас это очень даже устроило и мы поехали в Экибастуз. У нас был поезд, поэтому нас привезли на железнодорожный вокзал. Также мы проголодались, но неудобство небольших городов - это отсутствие мест, где можно покушать, т.к. все питаются дома. По крайней мере, мы не нашли возле вокзала нормального места покушать. В итоге решили пойти в сторону автовокзала и не ошиблись, через дорогу от автовокзала была кафешка, где мы пообедали. Далее вернулись на ж/д вокзал. Было очень тяжело в поезде, т.к. было очень нужно, в нашей секции плацкарта не открывалось окно :(.
Но не смотря на это, поездка удалась на славу 🙂
Если смотреть с берега, то кажется, что озеро куда-то сворачивает за горы. Но с горы уже видно, что перед нами полуостров, это потом уже вернувшить в Астану, я увидел на карте, что это остров. И назвается этот остров - "Остров влюбленных". Если бы мы знали раньше, что это остров, то прокатились бы до острова на катамаранах. А вообще люди на катамаранах плыли не к острову, а чуть поближе, к месту, где было не так глубоко, что даже было видно с высоты желтоватую воду. Возможно, в этом месте из воды выступали камни. Стоит немного рассказать о воде. Вода чистая, берег песчанный, дно тебя не засасывает, как в Боровом. Нужно довольно далеко отойти от берега, чтобы стало глубоко. Нырять с разбегу - не советую, так как на дне лежат большие камни. Да и плавать нужно осторожно, чтобы не наплыть на камень. Местами встречаются водоросли, поэтому приходилось смотреть в воду и высматривать камни и водоросли.
Людей тут очень мало, кто любит уединение - здесь понравиться.
Питание. По пути на пляж у нас была столовая, в которой можно было позавтракать, пообедать и поужинать, но в строго определенные для этого время. На территории есть мангал, но мясо нужно привозить с собой. Чтобы покушать шашлык и попить пиво также нужно идти в сторону трассы.
Теперь о возвращении. В день отъезда позвонили Бахи, он нашел нам попутное такси. Выйдя за территорию и немного пождав, подъехала машина, в которой были уже два пассажира. Я спросил столько с нас возьмут, оказалось еще дешевле 2000 с человека, нас это очень даже устроило и мы поехали в Экибастуз. У нас был поезд, поэтому нас привезли на железнодорожный вокзал. Также мы проголодались, но неудобство небольших городов - это отсутствие мест, где можно покушать, т.к. все питаются дома. По крайней мере, мы не нашли возле вокзала нормального места покушать. В итоге решили пойти в сторону автовокзала и не ошиблись, через дорогу от автовокзала была кафешка, где мы пообедали. Далее вернулись на ж/д вокзал. Было очень тяжело в поезде, т.к. было очень нужно, в нашей секции плацкарта не открывалось окно :(.
Но не смотря на это, поездка удалась на славу 🙂 Перебор всех возможных вариантов
В данной статье будет рассмотрено два алгоритма перебора всех возможных вариантов.
Для начала придумаем задачу, на примере которой будем рассматривать алгоритмы.
Пусть у нас имеется множество S, состоящее из 4-х элементов: * - + /, и наша задача - перебрать все возможные комбинации из 3-х элементов, используя элементы множества S. Причем, выбираемые элементы могут повторяться. Например: "+*+".
Первый алгоритм
Сопоставим каждому элементу число, начиная с 0.
* - 0
- - 1
+ - 2
/ - 3
Можно догадаться, что нужно перебрать элементы от 0 0 0 до 3 3 3:
0 0 0
0 0 1
0 0 2
0 0 3
0 1 0
0 0 1
...
...
3 2 3
3 3 0
3 3 1
3 3 2
3 3 3
Всего получится 64 варианта (4 * 4 * 4 = 64)
Далее нужно провести обратную операцию, сопоставив числу элемент множества S.
Например, набору 2 0 2 соответствует +*+
В алгоритме мы будем имитировать сложение в столбик, каждый раз прибавляя единицу, чтобы получить новый вариант.
Реализация:
char abc[] = new char[]{'*','-','+','/'};//множество допустимых символов
int size = 3;//кол-во элементов
int arr[] = new int[size];//массив для хранения текущего варианта множества
outer: while(true){//вечный цикл
//вывод варианта множества на экран
for(int ndx : arr){
System.out.print(abc[ndx]);
}
System.out.println();
int i = size - 1;//ставим курсов в самую правую ячейку
while(arr[i] == abc.length - 1){//движемся влево, если ячейка переполнена
arr[i] = 0;//записываем в ячейку 0, т.к. идет перенос разряда
i--;//сдвиг влево
//если перенос влево невозможен, значит перебор закончен
if(i < 0)break outer;
}
arr[i]++;//увеличиваем значение ячейки на единицу
}
В результате программа выведет все 64 варианта:
*** **- **+ **/ *-* *-- ... ... /++ /+/ //* //- //+ ///Второй алгоритм Для начала посчитаем сколько всего возможных комбинаций, это число равно n ^ k, где n - это размер алфавита (кол-во допустимых символов), а k - кол-во элементов в комбинации. Для нашего множества S, состоящего из *,-,+ и /, n равно 4. И т.к. нужно перебрать все комбинации из трех элементов, то k равно 3. Получаем: n ^ k = 4 ^ 3 = 64. В итоге мы должны получить 64 комбинации. Вот если бы существовал способ преобразования номера комбинации в элементы комбинации. И такой способ существует: для этого нужно номер комбинации преобразовать в k-значное число в системе счисления по основанию n. Первой комбинации будет соответствовать число 0, а последней 63. Перебирая числа от 0 до 63, нам нужно каждое число преобразовать в число в систему счисления по основанию 4. Для получения разрядов числа нужно целочисленно разделить число на 1, 4, 16 (т.е. n^0, n^1, n^2) и результат взять по модулю n. Пример: для числа 57 при k = 3 и n = 4 (57 / 1) % 4 = 57 % 4 = 1 (-) (57 / 4) % 4 = 14 % 4 = 2 (+) (57 / 16) % 4 = 3 % 4 = 3 (/) Т.е. комбинации под номером 57 соответствует комбинация -+/
char abc[] = new char[]{'*','-','+','/'};//множество допустимых символов (алфавит)
int N = abc.length;//N - размер алфавита
int K = 3;//кол-во элементов в комбинации
int pow[] = new int[K + 1];//массив для степеней числа N: N^0, N^1, .., N^K
pow[0] = 1;
for (int i = 1; i <= K; i++) {//вычисляем степени числа N
pow[i] = pow[i - 1] * N
}
//перебираем все номера комбинаций
for (int i = 0; i < pow[K]; i++) {
char arr[] = new char[K];
//вычисляем элементы комбинации
for (int j = 0; j < K; j++) {
//каждый элемент получаем из массива abc по индексу,
//индекс - это число в системе счисления по основанию N (0..N-1)
//в соответствующем разряде j (от 0 до K-1 включительно)
arr[j] = abc[(i / pow[j]) % N];
}
//вывод в консоль
for(char ch : arr){
System.out.print(ch);
}
System.out.println();
}
Вывод программы:
0 *** 1 -** 2 +** 3 /** 4 *-* ..... 57 -+/ 58 ++/ 59 /+/ 60 *// 61 -// 62 +// 63 ///В данном алгоритме перебор идет как бы слева направо, но это не важно, т.к. мы перебираем все комбинации.
No Carrier на Google Play
После публикации приложения на Google Play выяснилось, что на планшетах заказчика приложение не поддерживается. Причем мой планшет Asus поддерживается, а Samsung Galaxy Tab 4 не поддерживается, хотя там и там Android 4.4.2.
Если на Samsung Galaxy Tab искать приложение в Google Play, то оно не находится, т.к. не поддерживается. Если зайти на страничку приложения по ссылке, то можно увидеть сообщение "No Carrier". Сразу поняли, что дело в телефонных вызовах. У нас в приложении есть возможность набрать номер службы поддержки, поэтому в манифесте прописано разрешение:
Сперва подумали, что нужно вставить в планшет нормальную симку, а не LTE, но мой планшет вообще устанавливал приложение с Google Play без симки.
В итоге: где-то вычитал, что некоторые планшеты почему-то не могут совершать звонки.
Т.к. в нашем приложении вызов службы поддержки - это вспомогательный функционал, то прописали в манифесте необязательность телефонных вызовов:
После того, как прописали необязательность телефонных звонков, в Google Play к 5200-м поддерживаемым устройствам добавилось еще 500 устройств, в том числе Samsung Galaxy Tab 4. Проблема решилась!
Соответствие разрешений (uses-permission) и функций (uses-feature) можно посмотреть здесь:
http://developer.android.com/guide/topics/manifest/uses-feature-element.html#permissions-features