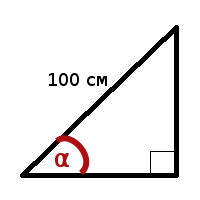
| Имеется прямоугольный треугольник, у которого гипотенуза равна 100 сантиметрам. Нужно вычислить при каком угле α площадь треугольника будет максимальна. |
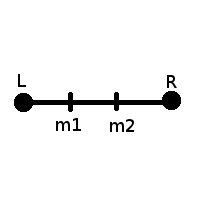Фрагмент кода, обеспечивающий равенство отрезков Lm1 = m1m2 = m2R:
double m1 = l + (r - l) / 3;
double m2 = r - (r - l) / 3;
При сравнении значений функций в точках m1 и m2 у нас возможно три варианта:
1) Мы сдвигаем область поиска вправо, т.е. l становится равным m1 (l = m1);
2) Мы сдвигаем область поиска влево, т.е. r становится равным m2 (r = m2);
3) При равенстве значений функции в обеих точках, мы сдвигаем область поиска с обеих сторон, т.е. l становиться равным m1 (l = m1), а r становиться равным m2 (r = m2)
Рассмотрим данные случаи на примере поиска максимального значения.
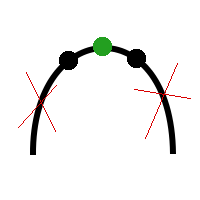
1) Если f(m1) < f(m2), возможно два случая: когда максимальное значение лежит в центральной части или в правой части, а значит левую часть можно отбросить. Максимальное значение обозначено зеленой точкой.
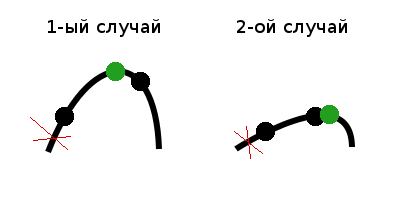2) Если f(m1) > f(m2), аналогично имеется только два случая, когда максимальное значение лежит в центральной или левой части, а значит правую часть можно отбросить.
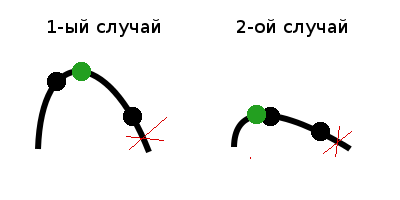3) Если f(m1) = f(m2), то возможен только один вариант, при котором максимальное значение находится в центральной части, а значит левую и правую части можно отбросить.
Последний вариант, когда f(m1) = f(m2), в целях облегчения алгоритма можно заменить либо на этот случай f(m1) < f(m2), либо на этот f(m1) > f(m2). В скорости из-за этого, конечно же, мы чуть-чуть проиграем, но выиграем в скорости реализации алгоритма и компактности кода.
После каждого шага алгоритма от исходной области поиска остается 2/3, т.е. не самая большая скорость сходимости. Можно повысить скорость сходимости, если выбирать точки m1 и m2 ближе друг другу, правда при этом теряется точность. Повышение скорости сходимости может потребоваться в случае, когда вычисление функции f(x) занимает много времени и нужно минимизировать кол-во вызовов этой функции.
Очень хорошо при выборе точек m1 и m2 воспользоваться пропорциями золотого сечения. Если тернарный поиск использует пропорции золотого сечения, то это один в один Метод золотого сечения.
Золотое сечение - это такое разбиение целого на две части, при котором отношение большего к меньшему равно отношению целого к большему
Это отношение постоянно и равно примерно 1,618, обозначается как φ и называется золотым числом:
Для вычисления точек m1 и m2, разбивающих область поиска золотым сечением, воспользуемся следующими формулами:
В процентном соотношении длины отрезков lm1 и lm2 приблизительно равны 38,2% и 61,8% от длины отрезка lr.
Благодаря свойствам золотого сечения точка m1 делит отрезок lm2 в пропорциях золотого сечения, а точка m2 делит отрезок m1r также в пропорциях золотого сечения.
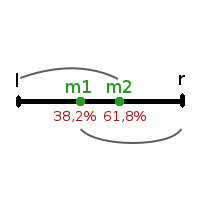И так мы видим, что сходимость золотого сечения будет 0,618, что лучше сходимости в случае разбиения области поиска на равные части, где сходимость у нас была 2/3 (0,66).
А теперь вернемся к решению задачи... Исходный код решения задачи на Java:
import static java.lang.Math.*;
public class angle {
public static void main(String[] args) {
double l = 0;
double r = 90;
double EPS = 1e-6;//точность 0.000001
double hypo = 100;//гипотенуза
while(r - l >= EPS){//повторяем цикл пока не достигнем требуемой точности
double m1 = l + (r - l) / 3;
double m2 = r - (r - l) / 3;
if(f(hypo,m1) < f(hypo,m2)){
l = m1;
}else{
r = m2;
}
}
System.out.println((l + r) / 2);//результат 44.99999993498489
}
//функция расчета площади треугольника по гипотенузе и углу
static double f(double hypo,double alpha){
alpha = toRadians(alpha);
return 0.5 * hypo * hypo * cos(alpha) * sin(alpha);
}
}
Т.е. при угле в 44.999999° (45°) достигается максимальная площадь треугольника. В качестве ответа можно было взять значение из переменной l или r, это возможно благодаря достижению заданной точности результата, также можно взять их середину (l + r) / 2, как в рассмотренном выше коде.
Задача на вложенный тернарный поиск
В качестве примера применения вложенного тернарного поиска возьмем задачу "Футбольные ворота". С условием задачи можно ознакомиться здесь или здесь.
Найти максимальную площадь ворот можно, подобрав углы для палок α и β:
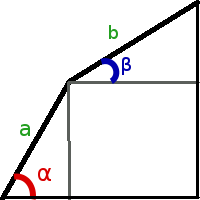Сперва мы находим углы α1 и α2, которые разбивают область поиска на три равные части (в данной задачи можно не использовать золотое сечение). Далее для угла α1 с помощью вложенного тернарного поиска ищем угол β1, при котором площадь фигуры максимальна, аналогично, для угла α2 находим подходящий угол β2.
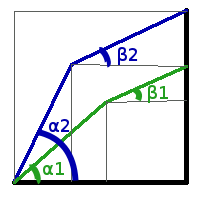Найдя пары углов α1 и β1; α2 и β2, вычисляем площадь S1 и S2 соответственно. Можно использовать следующую формулу вычисления площади, где a и b - длины палок:
S = 0.5 * a * a * cos(alpha) * sin(alpha) + 0.5 * b * b * cos(beta) * sin(beta) + a * b * sin(alpha) * cos(beta)Сравнив полученные площади, мы можем отсеять треть диапазона углов, которые дают маленькую площадь. И повторяем эти шаги до тех пор, пока не достигнем требуемой точности. Код решения задачи на Java:
import java.io.*;
import static java.lang.Math.*;
import java.text.DecimalFormat;
import java.text.DecimalFormatSymbols;
import java.util.*;
public class FooballGate {
static int a;//длина 1-ой палки
static int b;//длина 2-ой палки
static double EPS = 1e-6;//точность результата
public static void main(String[] args) throws IOException {
Scanner s = new Scanner(new File("input.txt"));
s.useLocale(Locale.US);
a = s.nextInt();
b = s.nextInt();
s.close();
double l = 0;
double r = 90;
while(r - l >= EPS){
double m1 = l + (r - l) / 3;
double m2 = r - (r - l) / 3;
if(f(m1) < f(m2)){
l = m1;
}else{
r = m2;
}
}
double ans = f((l + r) / 2);//результат
DecimalFormat df = new DecimalFormat("0.00000000",
DecimalFormatSymbols.getInstance(Locale.US));
System.out.println(df.format(ans));//вывод с восемью знаками после запятой
}
//функция расчета площади с фиксированным углом alpha,
//в которой тернарным поиском идет поиск угла beta,
//при котором площадь максимальна
static double f(double alpha){
double l = 0;
double r = 90;
while(r - l >= EPS){
double m1 = l + (r - l) / 3;
double m2 = r - (r - l) / 3;
if(f(alpha,l) < f(alpha,r)){
l = m1;
}else{
r = m2;
}
}
return f(alpha,(l + r) / 2);
}
//функция расчета площади в зависимости от углов: alpha и beta
static double f(double alpha, double beta){
alpha = toRadians(alpha);
beta = toRadians(beta);
return 0.5 * a * a * cos(alpha) * sin(alpha) +
0.5 * b * b * cos(beta) * sin(beta) +
a * b * sin(alpha) * cos(beta);
}
}
Задача на тройную вложенность тернарного поиска с необходимостью применения золотого сечения
Задача называется "Космические спасатели". Ознакомиться с условием задачи можно здесь или здесь.
По условию задачи нам нужно вычислить координаты x,y,z строительства новой спасательной станции, причем расстояние от станции до самой дальней планеты должно быть минимально.
Сперва пробуем подобрать координату x тернарным поиском, но координаты y и z - неизвестны, поэтому зафиксировав некоторые точки x, полученные золотым сечением, мы запускаем вложенные тернарный поиск с фиксированной координатой x для поиска координаты y. Далее внутри поиска y запускаем вложенный тернарный поиск координаты z. Когда мы имеем все три зафиксированные координаты мы можем посчитать расстояния до всех планет и из них определить максимальное расстояние, это расстояние и будет значением функции f(x,y,z).
Т.к. в условии сказано, что количество планет может быть 100, то вычисление функции f(x,y,z) очень затратно по времени. Чтобы программа уложилась во временные рамки, нужно при тернарном поиске разбивать область поиска золотым сечением, а не на равные части. Тем самым у нас повыситься сходимость, т.е. вызовов функции f(x,y,z) станет меньше. Но при золотом сечении теряется точность, поэтому мы увеличим точность с 10-6 до 10-7.
Реализация на Java:
import java.io.*;
import java.text.DecimalFormat;
import java.text.DecimalFormatSymbols;
import java.util.*;
public class SpaceRescuers {
static int MAX = (int) 1e4;//максимальная граница поиска
static int MIN = -MAX;//минимальная граница поиска
static class Point{
int x;
int y;
int z;
public Point(int x, int y, int z) {
super();
this.x = x;
this.y = y;
this.z = z;
}
}
static class PointD{
double x;
double y;
double z;
public PointD(double x, double y, double z) {
super();
this.x = x;
this.y = y;
this.z = z;
}
}
static Point[] points;
static double EPS = 1e-7;
static PointD bestPoint;//лучшая точка
static double best = Double.MAX_VALUE;//лучшее расстояние (минимальное)
static double fi = 1 / ((Math.sqrt(5) + 1) / 2);
public static void main(String[] args) throws IOException {
Scanner s = new Scanner(new File("input.txt"));
s.useLocale(Locale.US);
int N = s.nextInt();
points = new Point[N];
for(int i = 0; i < N; i++){
points[i] = new Point(s.nextInt(),s.nextInt(),s.nextInt());
}
s.close();
double l = MIN;
double r = MAX;
while(r - l > EPS){
double delta = (r - l) * fi;
double m1 = r - delta;
double m2 = l + delta;
if(f(m1) > f(m2)){
l = m1;
}else{
r = m2;
}
}
double x = bestPoint.x;
double y = bestPoint.y;
double z = bestPoint.z;
DecimalFormat df = new DecimalFormat("0.000000",
DecimalFormatSymbols.getInstance(Locale.US));
System.out.println(df.format(x) + " " + df.format(y) + " " +
df.format(z));
}
//опредение минимального расстояния при фиксированной координате x
static double f(double x){
double l = MIN;
double r = MAX;
while(r - l > EPS){
double delta = (r - l) * fi;
double m1 = r - delta;
double m2 = l + delta;
if(f(x,m1) > f(x,m2)){
l = m1;
}else{
r = m2;
}
}
return f(x,(l + r) / 2);
}
//определение минимального расстояния при фиксированных координатах x и y
static double f(double x,double y){
double l = MIN;
double r = MAX;
while(r - l > EPS){
double delta = (r - l) * fi;
double m1 = r - delta;
double m2 = l + delta;
if(f(x,y,m1) > f(x,y,m2)){
l = m1;
}else{
r = m2;
}
}
return f(x,y,(l + r) / 2);
}
//определение минимального расстояния при фиксированных координатах x,y и z
static double f(double x,double y,double z){
double max = 0;
for(int i = 0; i < points.length; i++){
Point p = points[i];
double s =
(p.x - x) * (p.x - x) +
(p.y - y) * (p.y - y) +
(p.z - z) * (p.z - z);
max = Math.max(max, s);
}
if(max < best){
best = max;
bestPoint = new PointD(x,y,z);
}
return max;
}
}
Обратите внимание на некоторые места в коде:
- Мы рассчитываем не φ, а 1/φ, чтобы дальше в вычислениях использовать умножение, а не деление, т.к. умножение работает быстрее;
static double fi = 1 / ((Math.sqrt(5) + 1) / 2);
double delta = (r - l) * fi; double m1 = r - delta; double m2 = l + delta;
- В первых двух задачах мы рассматривали поиск максимального значения, а данной задаче нас интересует минимально значение, поэтому в условном операторе меняется условие:
if(f(m1) > f(m2)){ l = m1; }else{ r = m2; } - Обратите внимание, что при расчете расстояния извлечение квадратного корня опущено.
double s = (p.x - x) * (p.x - x) + (p.y - y) * (p.y - y) + (p.z - z) * (p.z - z);
Извлечение квадратног корня - очень затратная операция. Сравнивать расстояния можно и без извлечения корня, а если бы потребовалось узнать самое минимальное расстояние, то корень можно было бы извлечь в самом конце.