Треугольник Паскаля имеет практическое применение в комбинаторике для нахождения сочетания из
n по
k.
Определение из Википедии:
В комбинаторике сочетанием из n по k называется набор k элементов, выбранных из данного множества, содержащего n различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Вы можете встретить два вида обозначения сочетения из
n по
k:
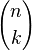
или
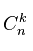
Давайте придумаем задачу.
Задача
Пусть у нас есть множество из 5 элементов: {1,2,3,4,5}.
Нужно найти кол-во сочетаний из трех элементов.
Причем наборы вида: {1,2,3} и {1,3,2} считаются одинаковыми и засчитываются только один раз.
Ответ
Из 5 элементов мы можем составить
10 наборов по 3 элемента.
Вот эти подмножества:
- {1,2,3}
- {1,2,4}
- {1,2,5}
- {1,3,4}
- {1,3,5}
- {1,4,5}
- {2,3,4}
- {2,3,5}
- {2,4,5}
- {3,4,5}
Решение
Задача сводится к нахождению сочетания из 5 по 3, т.е. n = 5, k = 3.
Для нахождения сочетания есть готовая формула:

Подставим наши значения в формулу:
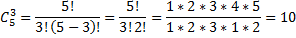
Пример реализации этой формулы на Java:
long C(int n,int k){
return fact(n) / (fact(k) * fact(n-k));
}
long fact(int num){
long val = 1;
for (int i = 2; i <= num; i++) {
val *= i;
}
return val;
}
Пример использования:
System.out.println(C(5,3));//возвратит 10
Вычисляя факториалы в формуле, мы проводим вычисления в числителе и знаменателе, и можно заметить, что некоторые операция умножения можно сократить.
Усовершенствованная версия:
long C(int n,int k){
int res = 1;
for (int i = n - k + 1; i <= n; i++) {
res *= i;
}
for (int i = 2; i <= k; i++) {
res /= i;
}
return res;
}
Основная сложность при расчетах - это вычисление факториала. Вычисление факториала числа - очень затратная операция, особенно, если у вас задача с расчетом большого кол-во сочетаний из
n по
k. Можно, конечно, кэшировать факториалы, но в формуле производятся и другие математические операции.
Кроме приведенной выше формулы с факториалами существует другой способ нахождения сочетания из
n по
k. Способ заключается в построении треугольника Паскаля, из которого уже берутся готовые значения.
Классический вид треугольника Паскаля:
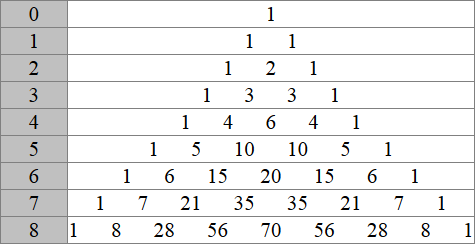 Как строится треугольник?
Как строится треугольник? Треугольник строится построчно сверху вниз. На вершине всегда единица. Каждый элемент в треугольнике получается сложением двух элементом, между которыми и под которыми лежит данный элемент. Причем боковые элементы получаются равными 1.
В программе мы будем хранить треугольник Паскаля в двумерном массиве, поэтому он несколько видоизменится:
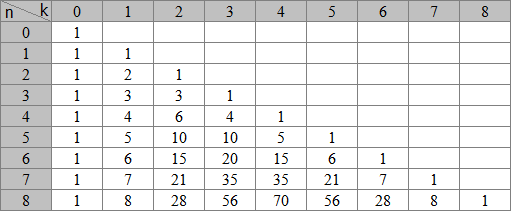
Элементы треугольника - это и есть наши искомые кол-ва сочетаний из
n по
k:
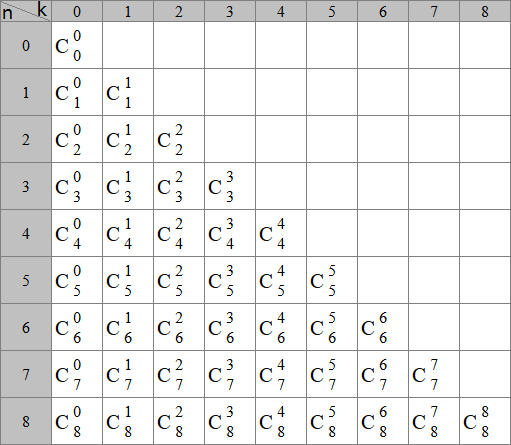 Теперь приступим к реализации
Теперь приступим к реализации
Треугольник будем хранить в двумерном массиве
C[][].
Нужно определиться с типом массива, так как числа будут получаться большими, будет переполнение переменных, а вы не заметите.
Приведу таблицу типов и предельных значений, после которых будет переполнение в элементах массива.
| Тип массива | Безопасный предел
|
|---|
| int | при n <= 33
|
| long | при n <= 66
|
| BigInteger | ограничено оперативной памятью
(ниже будет рассмотрено более подробно)
|
Реализация для
int и
long одинаковая, поэтому рассмотрим только
long , а вот для
BigInteger немного отличается.
Реализация с использованием long-массива:
public class PascalTriangle {
private int ubound;
private long C[][];
//инициализация треугольника
public PascalTriangle(int ubound){
if(ubound > 66){
throw new RuntimeException("Data overflow");
}
this.ubound = ubound;
C = new long[ubound+1][ubound+1];
for (int n = 0; n <= ubound; n++) {
//первый и последний элемент в строке равен 1
C[n][0] = C[n][n] = 1;
//далее вычисляем внутреннюю часть
for (int k = 1; k < n; k++) {
C[n][k] = C[n-1][k-1] + C[n-1][k];
}
}
}
//вывод треугольника в консоль
public void show(){
for (int n = 0; n <= ubound; n++) {
for (int k = 0; k <= n; k++) {
System.out.print(C[n][k] + " ");
}
System.out.println();
}
}
//метод, возвращающий кол-во сочетаний из n по k
public long get(int n,int k){
return C[n][k];
}
}
Пример использования:
PascalTriangle pas = new PascalTriangle(66);
//pas.show();
System.out.println(pas.get(5, 3));//результат 10
Теперь рассмотрим случай с
BigInteger.
BigInteger - это прекрасный класс Java по работе с длинными числами. Все числа хранятся внутри класса, а математические операции производятся с помощью методов класса. Например, операция сложения, которую мы применим в коде, производится с помощью метода
add.
public class BigPascalTriangle {
private int ubound;
private BigInteger C[][];
//инициализация треугольника
public BigPascalTriangle(int ubound){
this.ubound = ubound;
C = new BigInteger[ubound+1][ubound+1];
for (int n = 0; n <= ubound; n++) {
//первый и последний элемент в строке равен 1
C[n][0] = C[n][n] = BigInteger.ONE;
//далее вычисляем внутреннюю часть
for (int k = 1; k < n; k++) {
C[n][k] = C[n-1][k-1].add(C[n-1][k]);//аналог C[n][k] = C[n-1][k-1] + C[n-1][k] для длинной арифметики
}
}
}
//вывод треугольника в консоль
public void show(){
for (int n = 0; n <= ubound; n++) {
for (int k = 0; k <= n; k++) {
System.out.print(C[n][k] + " ");
}
System.out.println();
}
}
//метод, возвращающий кол-во сочетаний из n по k
public BigInteger get(int n,int k){
return C[n][k];
}
}
Пример использования:
BigPascalTriangle pas = new BigPascalTriangle(100);
pas.show();
System.out.println(pas.get(5, 3));//результат 10
Теперь о минусах, точнее минусе.
Построение треугольника требует затрат оперативной памяти.
Для массива
long при
n <= 66 - это неощутимо.
Но для реализации с
BigInteger - ощутимо, и при не хватке памяти будет выброшена ошибка:
java.lang.OutOfMemoryError: Java heap space
Ниже я приведу табличку с примерными ограничениями.
Внимание! Данные приведены только с учетом построения треугольника, без учета того, что вы можете хранить в программе еще другие данные. Также данные могут отличаться, т.к. на приграничных значениях программа может то выбрасывать исключение, то не выбрасывать. Время построения треугольника тоже варьируется. Поэтому данные примерные!
| Оперативная память | Допустимое значение | Время построения треугольника
|
|---|
| 256 МБ | n = 1700 | 840 мс
|
| 512 МБ | n = 2150 | 1200 мс
|
| 1024 МБ | n = 2960 | 3700 мс
|
| 2048 МБ | n = 3470 | 7200 мс
|
| 4096 МБ | n = 4340 | 16000 мс
|
p.s. Треугольник Паскаля можно применять для решения и других задач.
В заключении приведу цитату Мартина Гарднера о треугольнике Паскаля:
Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В то же время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике.