НОД (Наибольший общий делитель) или gcd (Greatest Common Divisor)
НОД - наибольшее число, которое является делителем одновременно для чисел
a и
b.
Реализация (Алгоритм Евклида):
long gcd(long a,long b){
return b == 0 ? a : gcd(b,a % b);
}
Применение:
System.out.println(gcd(10,24));//результат: 2
System.out.println(gcd(12,24));//результат: 12
System.out.println(gcd(11,24));//результат: 1
НОК (Наименьшее общее кратное) или lcm (Least Common Multiple)
НОК - наименьшее число, которое делится на
a и
b без остатка.
НОК можно найти через НОД по следующей формуле:
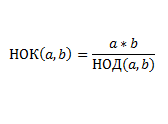
Реализация:
long lcm(long a,long b){
return a / gcd(a,b) * b;
}
Примечание:
a / gcd(a,b) * b более предпочтительно, чем
a * b / gcd(a,b), т.к. во втором случае при больших числах переполнение случиться намного раньше.
Применение:
System.out.println(lcm(3, 4));//результат: 12
System.out.println(lcm(3, 9));//результат: 9
System.out.println(lcm(5,12));//результат: 60
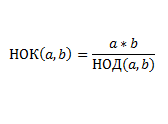 Реализация:
Реализация:
Добавить комментарий